(年新疆、生产建设兵团)已知,AC∥ED,∠C=26°,∠CBE=37°,则∠BED的度数是( )
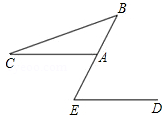
| A.53° | B.63° | C.73° | D.83° |
(年新疆乌鲁木齐市)如图,△ABC的面积等于6,边AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,点P在直线AD上,则线段BP的长不可能是( )

| A.3 | B.4 | C.5 | D.6 |
(年云南省昆明市)如图,在△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为( )
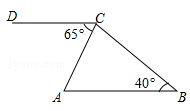
| A.60° | B.65° | C.70° | D.75° |
(年贵州省遵义市)有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3 、7
、7 、9
、9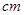 ;乙盒子中装有4张卡片,卡片上分别写着2
;乙盒子中装有4张卡片,卡片上分别写着2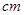 、4
、4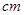 、6
、6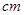 、8
、8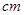 ;盒子外有一张写着5
;盒子外有一张写着5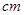 的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率.
(年贵州省黔东南州)如图,已知二次函数 的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为
的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为 .
.
(1)求二次函数 的解析式及点B的坐标;
的解析式及点B的坐标;
(2)由图象写出满足 的自变量x的取值范围;
的自变量x的取值范围;
(3)在两坐标轴上是否存在点P,使得△ABP是以AB为底边的等腰三角形?若存在,求出P的坐标;若不存在,说明理由.
(年青海省中考)如图,二次函数 的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
(1)求该抛物线的解析式;
(2)判断△BCM的形状,并说明理由;
(3)探究坐标轴上是否存在点P,使得以点P、A、C为顶点的三角形与△BCM相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
(年新疆乌鲁木齐市)如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )

A.( ,1) ,1) |
B.(1, ) ) |
C.( ,﹣2) ,﹣2) |
D.(2, ) ) |
(年贵州省黔东南州)如图,在△ABO中,AB⊥OB,OB= ,AB=1.将△ABO绕O点旋转90°后得到△A1B1O,则点A1的坐标为( )
,AB=1.将△ABO绕O点旋转90°后得到△A1B1O,则点A1的坐标为( )

A.( , , ) ) |
B.( , , )或(1, )或(1, ) ) |
C.( , , ) ) |
D.( , , )或( )或( , , ) ) |
(本小题满分10分)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D
以AB上一点O为圆心作⊙O,使⊙O经过点A和点D。
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°,
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD,BE与劣弧 所围成的阴影部分的面积(结果保留根号和
所围成的阴影部分的面积(结果保留根号和 )。
)。
(贵州省安顺市)(本题12分)
如图,等腰三角形ABC中,AC=BC=10,AB=12.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
(1)求证:直线EF是⊙O的切线;
(2)求 的值.
的值.
(黔西南州)如图所示,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切
(2)PO的延长线与⊙O交于点E,若⊙O的半径为3,PC=4.求弦CE的长.
如图,已知在△ABC中,∠A=90°,
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明).
(2)若∠B=60°,AB=3,求⊙P的面积.
(本小题5分)如图,在图中求作⊙P,使⊙P满足以线段MN为弦,且圆心P到∠AOB两边的距离相等(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)。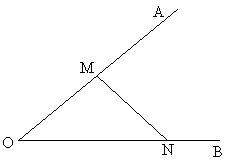
已知关于x的方程x2-(m+2)x+(2m-1)=0的一个根是2,请求出方程的另一个根,并求以此两根为边长的直角三角形的面积。
如图,正方形ABCD的边长为1,分别以AB,BC,CD,DA为斜边作等腰直角三角形顺次得到第一个正方形A1B1C1D1,分别以A1B1,B1C1,C1D1,D1A1为斜边作等腰直角三角形顺次得到第二个正方形A2B2C2D2,…,以此类推,则第六个正方形A2014B2014C2014D2014面积是 。
