在Rt△ ABC中,∠ C=90°, AD平分∠ CAB, BE平分∠ ABC, AD、 BE相交于点 F,且 AF=4, EF= ,则 AC= .

如图1,直角三角形纸片的一条直角边长为2,剪四块这样的直角三角形纸片,把它们按图2放入一个边长为3的正方形中(纸片在结合部分不重叠无缝隙),则图2中阴影部分面积为 .

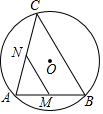
如图, 是 的弦, ,点 是 上的一个动点,且 ,若点 、 分别是 、 的中点,则 长的最大值是 .
已知正方形 ABCD的面积是2, E为正方形一边 BC在从 B到 C方向的延长线上的一点,若 CE= ,连接 AE,与正方形另外一边 CD交于点 F,连接 BF并延长,与线段 DE交于点 G,则 BG的长为 .
如图,矩形 中, , , 是 的中点,直线 平行于直线 ,且直线 与直线 之间的距离为2,点 在矩形 边上,将矩形 沿直线 折叠,使点 恰好落在直线 上,则 的长为 .

如图, 中,点 为边 的中点,连接 ,将 沿直线 翻折至 所在平面内,得 ,连接 ,分别与边 交于点 ,与 交于点 .若 , ,则 的长为 .

如图, 与 的边 相切,切点为 .将 绕点 按顺时针方向旋转得到△ ,使点 落在 上,边 交线段 于点 .若 ,则
度.
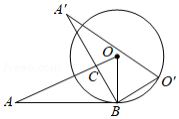
图1是一种矩形时钟,图2是时钟示意图,时钟数字2的刻度在矩形 的对角线 上,时钟中心在矩形 对角线的交点 上.若 ,则 长为 (结果保留根号).
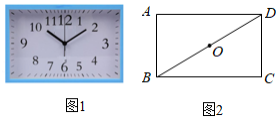
如图,在河对岸有一矩形场地 ,为了估测场地大小,在笔直的河岸 上依次取点 , , ,使 , ,点 , , 在同一直线上.在 点观测 点后,沿 方向走到 点,观测 点发现 .测得 米, 米, 米, ,则场地的边 为 米, 为 米.
