如图,正方形 中, 是对角线 上一点,且 ,则 的度数为

A. B. C. D.
如图,菱形 的对角线 、 相交于点 ,点 为边 的中点,若菱形 的周长为16, ,则 的面积是

A. B.2C. D.4
若实数 、 满足等式 ,且 、 恰好是等腰 的两条边的边长,则 的周长是
A.12B.10C.8D.6
如图,在 中,延长 至 ,使得 ,过 中点 作 (点 位于点 右侧),且 ,连接 .若 ,则 的长为

A.3B.4C. D.
如图, 中, , 平分 交 于点 ,按下列步骤作图:
步骤1:分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于 , 两点;
步骤2:作直线 ,分别交 , 于点 , ;
步骤3:连接 , .
若 , ,则线段 的长为

A. B. C. D.
下列长度的三条线段能组成直角三角形的是
A . 3 , 4 , 5B . 2 , 3 , 4C . 4 , 6 , 7D . 5 , 11 , 12
如图, ,且 . 、 是 上两点, , .若 , , ,则 的长为
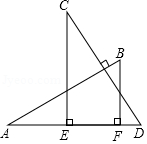
A. B. C. D.
如图,菱形 的对角线 、 的长分别为6和8,则这个菱形的周长是

A.20B.24C.40D.48
我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若 , ,则该矩形的面积为
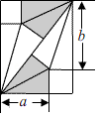
A.20B.24C. D.
如图,等边三角形 边长是定值,点 是它的外心,过点 任意作一条直线分别交 , 于点 , .将 沿直线 折叠,得到△ ,若 , 分别交 于点 , ,连接 , ,则下列判断错误的是

A.
B.△ 的周长是一个定值
C.四边形 的面积是一个定值
D.四边形 的面积是一个定值
如图, 是 的直径,弦 于 ,连接 ,过点 作 于 ,若 , ,则 的长度是
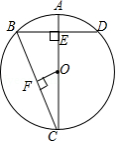
A. B. C. D.
如图,在 中, , , ,以点 为圆心, 长为半径画弧,交边 于点 ,则 的长为

A. B. C. D.
如图,在 中,对角线 与 相交于点 , 是边 的中点,连接 .若 , ,则 的度数为

A. B. C. D.