初中数学认识立体图形试题

下列四个几何体中，是三棱柱的为 $($　　 $)$

A．B．

C．D．

某几何体的三视图如图所示，则下列说法错误的是 $($ 　　 $)$

A．	该几何体是长方体
B．	该几何体的高是3
C．	底面有一边的长是1
D．	该几何体的表面积为18平方单位

下列图形中，属于立体图形的是 $($　　 $)$

A．B．C．D．

不透明袋子中装有一个几何体模型，两位同学摸该模型并描述它的特征．甲同学：它有4个面是三角形；乙同学：它有8条棱．该模型的形状对应的立体图形可能是 $($　　 $)$

A．三棱柱B．四棱柱C．三棱锥D．四棱锥

下列几何体中，是圆柱的为 $($ 　　 $)$

A．		B．
C．		D．

下列图形中，属于立体图形的是 $($　　 $)$

A．B．C．D．

如图，这是一个底面为等边三角形的正三棱柱和它的主视图、俯视图，则它的左视图的面积是 $($ 　　 $)$

A．

4

B．

2

C．

$\sqrt{3}$

D．

$2\sqrt{3}$

围成下列立体图形的各个面中，每个面都是平的是（　　）

A．	长方体	B．	圆柱体
C．	球体	D．	圆锥体

问题提出：

如图，图①是一张由三个边长为1的小正方形组成的“”形纸片，图②是一张的方格纸的方格纸指边长分别为，的矩形，被分成个边长为1的小正方形，其中，，且，为正整数）．把图①放置在图②中，使它恰好盖住图②中的三个小正方形，共有多少种不同的放置方法？

问题探究：

为探究规律，我们采用一般问题特殊化的策略，先从最简单的情形入手，再逐次递进，最后得出一般性的结论．

探究一：

把图①放置在的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？

如图③，对于的方格纸，要用图①盖住其中的三个小正方形，显然有4种不同的放置方法．

探究二：

把图①放置在的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？

如图④，在的方格纸中，共可以找到2个位置不同的方格，依据探究一的结论可知，把图①放置在的方格纸中，使它恰好盖住其中的三个小正方形，共有种不同的放置方法．

探究三：

把图①放置在的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？

如图⑤，在的方格纸中，共可以找到　　个位置不同的方格，依据探究一的结论可知，把图①放置在的方格纸中，使它恰好盖住其中的三个小正方形，共有　　种不同的放置方法．

探究四：

把图①放置在的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？

如图⑥，在的方格纸中，共可以找到　　个位置不同的方格，依据探究一的结论可知，把图①放置在的方格纸中，使它恰好盖住其中的三个小正方形，共有　　种不同的放置方法．

问题解决：

把图①放置在的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？（仿照前面的探究方法，写出解答过程，不需画图．

问题拓展：

如图，图⑦是一个由4个棱长为1的小立方体构成的几何体，图⑧是一个长、宽、高分别为，，，，，且，，是正整数）的长方体，被分成了个棱长为1的小立方体．在图⑧的不同位置共可以找到　　个图⑦这样的几何体．

已知圆柱的底面积为 $60c{m}^2$，高为 $4\mathit{cm}$，则这个圆柱体积为　　 $c{m}^3$．

如图，是一个几何体从正面、左面、上面看得到的平面图形，判断下面说法的正误（正确的在括号内划△，错误的在括号内划）

（1）这是一个棱锥________．
（2）这个几何体有4个面________．
（3）这个几何体有5个顶点________．
（4）这个几何体有8条棱________．
（5）请你再说出一个正确的结论________．

下列说法中：
①棱柱的上、下底面的形状相同；
②若AB=BC，则点B为线段AC的中点；
③相等的两个角一定是对顶角；
④不相交的两条直线叫做平行线；
⑤直线外一点与直线上各点连接的所有线段中，垂线段最短。
正确的有（    ）

A．1个

B．2个

C．3个

D．4个

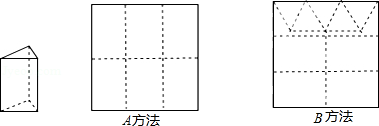
用边长为12cm的正方形硬纸板做三棱柱盒子，每个盒子的侧面为长方形，底面为等边三角形．
（1）每个盒子需      个长方形，      个等边三角形；
（2）硬纸板以如图两种方法裁剪（裁剪后边角料不再利用）A方法：剪6个侧面；B方法：剪4侧面5个底面．

现有19张硬纸板，裁剪时x张用A方法，其余用B方法．
①用x的代数式分别表示裁剪出的侧面和底面的个数；
②若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？

如图，以边长为 $20\mathit{cm}$的正三角形纸板的各顶点为端点，在各边上分别截取 $4\mathit{cm}$长的六条线段，过截得的六个端点作所在边的垂线，形成三个有两个直角的四边形．把它们沿图中虚线剪掉，用剩下的纸板折成一个底为正三角形的无盖柱形盒子，则它的容积为　    　 $c{m}^3$．

有一个正六面体骰子（如图a）放在桌面上，将骰子沿如图所示的顺时针方向滚动，每滚动90°算一次，则滚动第2015次后，骰子朝下一面的点数是            ．