初中数学反比例函数的性质试题

如图，在平面直角坐标系中，函数的图象与等边三角形的边，分别交于点，，且，若，那么点的横坐标为　　．

如图，在平面直角坐标系中，点 $B$ 在第一象限， $\mathit{BA}\perp x$ 轴于点 $A$ ，反比例函数 $y=\frac{k}{x}(x>0)$ 的图象与线段 $\mathit{AB}$ 相交于点 $C$ ，且 $C$ 是线段 $\mathit{AB}$ 的中点，点 $C$ 关于直线 $y=x$ 的对称点 $C^{\text{'}}$ 的坐标为 $(1$ ， $n\left)\right(n\ne 1)$ ，若 $\mathit{\Delta OAB}$ 的面积为3，则 $k$ 的值为 $($ 　　 $)$

A．

$\frac{1}{3}$

B．

1

C．

2

D．

3

如图所示，在平面直角坐标系 $\mathit{xOy}$ 中，点 $A$ 、 $B$ 、 $C$ 为反比例函数 $y=\frac{k}{x}(k>0)$ 上不同的三点，连接 $\mathit{OA}$ 、 $\mathit{OB}$ 、 $\mathit{OC}$ ，过点 $A$ 作 $\mathit{AD}\perp y$ 轴于点 $D$ ，过点 $B$ 、 $C$ 分别作 $\mathit{BE}$ ， $\mathit{CF}$ 垂直 $x$ 轴于点 $E$ 、 $F$ ， $\mathit{OC}$ 与 $\mathit{BE}$ 相交于点 $M$ ，记 $\mathit{\Delta AOD}$ 、 $\mathit{\Delta BOM}$ 、四边形 $\mathit{CMEF}$ 的面积分别为 $S_1$ 、 $S_2$ 、 $S_3$ ，则 $($ 　　 $)$

A．

$S_1=S_2+S_3$

B．

$S_2=S_3$

C．

$S_3>S_2>S_1$

D．

$S_1{S}_2<S_3^2$

如图， $\odot O$ 的半径为2，双曲线的解析式分别为 $y=\frac{1}{x}和y=-\frac{1}{x}$ ，则阴影部分的面积是 $($ 　　 $)$

A．

$4\pi$

B．

$3\pi$

C．

$2\pi$

D．

$\pi$

若一个函数当自变量在不同范围内取值时，函数表达式不同，我们称这样的函数为分段函数．下面我们参照学习函数的过程与方法，探究分段函数的图象与性质．列表：

								0		1		2		3
				1		2		1		0		1		2

描点：在平面直角坐标系中，以自变量的取值为横坐标，以相应的函数值为纵坐标，描出相应的点，如图所示．

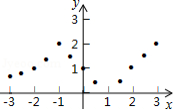
（1）如图，在平面直角坐标系中，观察描出的这些点的分布，作出函数图象；

（2）研究函数并结合图象与表格，回答下列问题：

①点，，，，，，在函数图象上，则　　，　　；（填“”，“ ”或“”

②当函数值时，求自变量的值；

③在直线的右侧的函数图象上有两个不同的点，，，，且，求的值；

④若直线与函数图象有三个不同的交点，求的取值范围．

如图，点，分别是正比例函数的图象与反比例函数的图象的交点，过点作轴于点，过点作轴于点，则四边形的面积为　　．

如图，一次函数的图象与反比例函数在第一象限的图象交于和两点，与轴交于点．

（1）求反比例函数的解析式；

（2）若点在轴上，且的面积为5，求点的坐标．

如图，△ $O{A}_1{B}_1$ ，△ $A_1{A}_2{B}_2$ ，△ $A_2{A}_3{B}_3$ ， $\dots$ 是分别以 $A_1$ ， $A_2$ ， $A_3$ ， $\dots$ 为直角顶点，一条直角边在 $x$ 轴正半轴上的等腰直角三角形，其斜边的中点 $C_1(x_1$ ， $y_1)$ ， $C_2(x_2$ ， $y_2)$ ， $C_3(x_3$ ， $y_3)$ ， $\dots$ 均在反比例函数 $y=\frac{4}{x}(x>0)$ 的图象上．则 $y_1+y_2+\dots +y_{10}$ 的值为 $($ 　　 $)$

A．

$2\sqrt{10}$

B．

6

C．

$4\sqrt{2}$

D．

$2\sqrt{7}$

如图，中，，顶点，分别在反比例函数与的图象上，则的值为　　．

如图，在平面直角坐标系中，点，在反比例函数的图象上运动，且始终保持线段的长度不变．为线段的中点，连接．则线段长度的最小值是　　（用含的代数式表示）．

如图，点，，是直线与反比例函数图象的两个交点，轴，垂足为点，已知，连接，，．

（1）求直线的表达式；

（2）和的面积分别为，．求．

如图，中，顶点的坐标是，轴，交轴于点，顶点的纵坐标是，的面积是24．反比例函数的图象经过点和，求：

（1）反比例函数的表达式；

（2）所在直线的函数表达式．

在下列函数图象上任取不同两点 $P_1(x_1$ ， $y_1)$ 、 $P_2(x_2$ ， $y_2)$ ，一定能使 $\frac{y_2-y_1}{x_2-x_1}<0$ 成立的是 $($ 　　 $)$

A．	$y=3x-1(x<0)$	B．	$y=-x^2+2x-1(x>0)$
C．	$y=-\frac{\sqrt{3}}{x}(x>0)$	D．	$y=x^2-4x+1(x<0)$

如图，在平面直角坐标系中，菱形 $\mathit{OABC}$ 的边 $\mathit{OA}$ 在 $x$ 轴的正半轴上，反比例函数 $y=\frac{k}{x}(x>0)$ 的图象经过对角线 $\mathit{OB}$ 的中点 $D$ 和顶点 $C$ ．若菱形 $\mathit{OABC}$ 的面积为12，则 $k$ 的值为 $($ 　　 $)$

A．

6

B．

5

C．

4

D．

3

如图，在平面直角坐标系中，矩形的顶点落在坐标原点，点、点分别位于轴，轴的正半轴，为线段上一点，将沿翻折，点恰好落在对角线上的点处，反比例函数经过点．二次函数的图象经过、、三点，则该二次函数的解析式为　　．（填一般式）