初中数学一次函数图象上点的坐标特征试题

设点 $A(-3,a)$ ， $B(b,\frac{1}{2})$ 在同一个正比例函数的图象上，则 $\mathit{ab}$ 的值为 $($ 　　 $)$

A．

$-\frac{2}{3}$

B．

$-\frac{3}{2}$

C．

$-6$

D．

$\frac{3}{2}$

一个不透明的口袋中装有三个除所标数字外完全相同的小球， 小球上分别标有数字， 0 ， 1 ． 从袋中一次随机摸出两个小球， 把上面标注的两个数字分别作为点的横、 纵坐标 ．

（1） 请用列表或画树状图的方法列出点所有可能的坐标；

（2） 求点在直线上的概率 ．

如图，在平面直角坐标系中，点、的坐标分别为、，若直线与线段有公共点，则的值可以为　　．（写出一个即可）

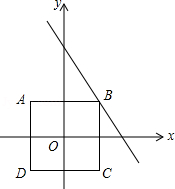
如图，在平面直角坐标系中，正方形的对称中心与原点重合，顶点的坐标为，顶点在第一象限，若点在直线上，则的值为　　．

对于题目"一段抛物线 $L:y=-x(x-3)+c(0⩽x⩽3)$ 与直线 $l:y=x+2$ 有唯一公共点，若 $c$ 为整数，确定所有 $c$ 的值，"甲的结果是 $c=1$ ，乙的结果是 $c=3$ 或4，则 $($ 　　 $)$

A．	甲的结果正确
B．	乙的结果正确
C．	甲、乙的结果合在一起才正确
D．	甲、乙的结果合在一起也不正确

如图，直角坐标系中，，直线与轴交于点，直线与轴及直线分别交于点，，点，关于轴对称，连接．

（1）求点，的坐标及直线的解析式；

（2）设面积的和，求的值；

（3）在求（2）中时，嘉琪有个想法：“将沿轴翻折到的位置，而与四边形拼接后可看成，这样求便转化为直接求的面积不更快捷吗？”但大家经反复演算，发现，请通过计算解释他的想法错在哪里．

在平面直角坐标系中，直线与直线，直线分别交于点，，直线与直线交于点．

（1）求直线与轴的交点坐标；

（2）横、纵坐标都是整数的点叫做整点，记线段，，围成的区域（不含边界）为．

①当时，结合函数图象，求区域内的整点个数；

②若区域内没有整点，直接写出的取值范围．