已知 P= ﹣ ( a≠± b)
(1)化简 P;
(2)若点( a, b)在一次函数 y= x﹣ 的图象上,求 P的值.
把函数 y= x向上平移3个单位,下列在该平移后的直线上的点是( )
| A. |
(2,2) |
B. |
(2,3) |
C. |
(2,4) |
D. |
(2,5) |
如图,有一条折线 A 1 B 1 A 2 B 2 A 3 B 3 A 4 B 4…,它是由过 A 1(0,0), B 1(4,4), A 2(8,0)组成的折线依次平移8,16,24,…个单位得到的,直线 y= kx+2( k<0)与此折线有2 n( n≥1且为整数)个交点,则 k的值为 .

阅读下面材料:
我们知道一次函数 y= kx+ b( k≠0, k、 b是常数)的图象是一条直线,到高中学习时,直线通常写成 Ax+ By+ C=0( A≠0, A、 B、 C是常数)的形式,点 P( x 0, y 0)到直线 Ax+ By+ C=0的距离可用公式 d= 计算.
例如:求点 P(3,4)到直线 y=﹣2 x+5的距离.
解:∵ y=﹣2 x+5
∴2 x+ y﹣5=0,其中 A=2, B=1, C=﹣5
∴点 P(3,4)到直线 y=﹣2 x+5的距离为:
根据以上材料解答下列问题:
(1)求点 Q(﹣2,2)到直线3 x﹣ y+7=0的距离;
(2)如图,直线 y=﹣ x沿 y轴向上平移2个单位得到另一条直线,求这两条平行直线之间的距离.

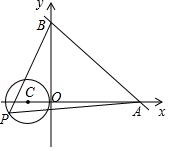
如图,直线 y=﹣ x+3与 x轴、 y轴分别交于 A、 B两点,点 P是以 C(﹣1,0)为圆心,1为半径的圆上一点,连接 PA, PB,则△ PAB面积的最小值是( )
| A. |
5 |
B. |
10 |
C. |
15 |
D. |
20 |
如图,直线l: ,点A1坐标为(﹣3,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2016的坐标为 .

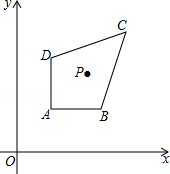
如图,在平面直角坐标系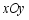 中,已知点
中,已知点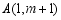 ,
,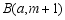 ,
,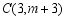 ,
,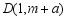 ,
,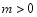 ,
,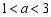 ,点
,点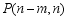 是四边形
是四边形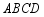 内的一点,且
内的一点,且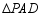 与
与 的面积相等,求
的面积相等,求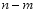 的值.
的值.
如图,在平面直角坐标系中,过点 的直线
的直线 与
与 轴交于点
轴交于点 ,
,直线
,
,直线 上的点
上的点 位于
位于 轴左侧,且到
轴左侧,且到 轴的距离为1.
轴的距离为1.
(1)求直线 的表达式;
的表达式;
(2)若反比例函数
的图象经过点 ,求
,求 的值.
的值.

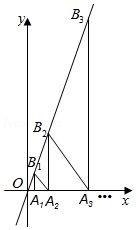
如图,在坐标轴上取点A1(2,0),作x轴的垂线与直线y=2x交于点B1,作等腰直角三角形A1B1A2;又过点A2作x轴的垂线交直线y=2x交于点B2,作等腰直角三角形A2B2A3;…,如此反复作等腰直角三角形,当作到An(n为正整数)点时,则An的坐标是 .
已知正比例函数y=3x的图象经过点(1,m),则m的值为( )
A. B.3C.﹣ D.﹣3
如图,在平面直角坐标系中,正方形 的顶点 与坐标原点重合,点 的坐标为 ,点 在 轴的正半轴上.直线 分别与边 , 相交于 , 两点,反比例函数 的图象经过点 并与边 相交于点 ,连接 .点 是直线 上的动点,当 时,点 的坐标是 .

如图,在平面直角坐标系中,一次函数 的图象与 轴、 轴分别相交于点 ,点 ,以线段 为边作正方形 ,且点 在反比例函数 的图象上,则 的值为

| A. |
|
B. |
|
C. |
42 |
D. |
|
如图,在平面直角坐标系中, 是直线 上的一个动点,将 绕点 顺时针旋转 ,得到点 ,连接 ,则 的最小值为

| A. |
|
B. |
|
C. |
|
D. |
|