如图1,点 是半圆 的直径 上一动点(不包括端点), ,过点 作 交半圆于点 ,连结 ,过点 作 交半圆于点 ,连结 .牛牛想探究在点 运动过程中 与 的大小关系.他根据学习函数的经验,记 , , .请你一起参与探究函数 、 随自变量 变化的规律.
通过几何画板取点、画图、测量,得出如下几组对应值,并在图2中描出了以各对对应值为坐标的点,画出了不完整图象.
|
|
|
0.30 |
0.80 |
1.60 |
2.40 |
3.20 |
4.00 |
4.80 |
5.60 |
|
|
|
|
2.01 |
2.98 |
3.46 |
3.33 |
2.83 |
2.11 |
1.27 |
0.38 |
|
|
|
|
5.60 |
4.95 |
3.95 |
2.96 |
2.06 |
1.24 |
0.57 |
0.10 |
|
(1)当 时, .
(2)在图2中画出函数 的图象,并结合图象判断函数值 与 的大小关系.
(3)由(2)知" 取某值时,有 ".如图3,牛牛连结了 ,尝试通过计算 , 的长来验证这一结论,请你完成计算过程.
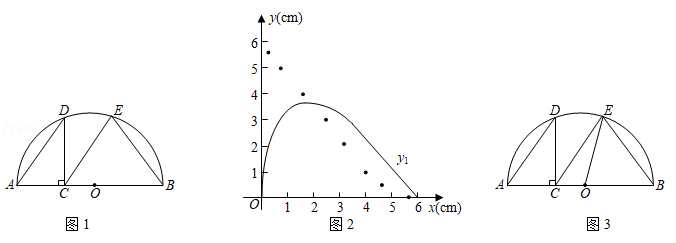
如图, 的顶点坐标分别为 , , ,动点 、 同时从点 出发,分别沿 轴正方向和 轴正方向运动,速度分别为每秒3个单位和每秒2个单位,点 到达点 时点 、 同时停止运动.过点 作 分别交 、 于点 、 ,连接 、 .设运动时间为 (秒 .
(1)求点 的坐标(用含 的式子表示);
(2)求四边形 面积的最大值或最小值;
(3)是否存在这样的直线 ,总能平分四边形 的面积?如果存在,请求出直线 的解析式;如果不存在,请说明理由;
(4)连接 ,当 时,求点 到 的距离.

如图1,在 中, , , ,点D为AB的中点,线段 上有一动点E,连接DE,作DA关于直线DE的对称图形,得到 ,过点F作 于点G.设A、E两点间的距离为 , 两点间的距离为
小军根据学习函数的经验,对因变量y随自变量x的变化而变化的规律进行了探究.
下面是小军的探究过程,请补充完整.

(1)列表:如表的已知数据是根据A,E两点间的距离x进行取点、画图、测量,分别得到了x与y的几组对应值:
x/cm |
0 |
0.51 |
1.03 |
1.41 |
1.50 |
1.75 |
2.20 |
2.68 |
3.00 |
3.61 |
4.10 |
4.74 |
5.00 |
y/cm |
0 |
0.94 |
1.91 |
2.49 |
|
2.84 |
3.00 |
2.84 |
2.60 |
2.00 |
1.50 |
0.90 |
0.68 |
请你通过计算补全表格;
(2)描点、连线:在平面直角坐标系 中(如图2),描出表中各组数值所对应的点 ,并画出y关于x的图象;
(3)探究性质:随着x值的不断增大,y的值是怎样变化的? ;
(4)解决问题:当 时,FG的长度大约是 cm(保留两位小数).
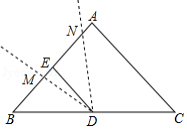
小亮在学习中遇到这样一个问题:
如图,点 是 上一动点,线段 ,点 是线段 的中点,过点 作 ,交 的延长线于点 .当 为等腰三角形时,求线段 的长度.
小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题.请将下面的探究过程补充完整:
(1)根据点 在 上的不同位置,画出相应的图形,测量线段 , , 的长度,得到下表的几组对应值.
|
0 |
1.0 |
2.0 |
3.0 |
4.0 |
5.0 |
6.0 |
7.0 |
8.0 |
|
8.0 |
7.7 |
7.2 |
6.6 |
5.9 |
|
3.9 |
2.4 |
0 |
|
8.0 |
7.4 |
6.9 |
6.5 |
6.1 |
6.0 |
6.2 |
6.7 |
8.0 |
操作中发现:
①“当点 为 的中点时, ”.则上表中 的值是 5.0 ;
②“线段 的长度无需测量即可得到”.请简要说明理由.
(2)将线段 的长度作为自变量 , 和 的长度都是 的函数,分别记为 和 ,并在平面直角坐标系 中画出了函数 的图象,如图所示.请在同一坐标系中画出函数 的图象;
(3)继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当 为等腰三角形时,线段 长度的近似值(结果保留一位小数).


如图,在 中, , ,点 为 的中点, ,将 绕点 顺时针旋转 度 ,角的两边分别交直线 于 、 两点,设 、 两点间的距离为 , , 两点间的距离为 .
小涛根据学习函数的经验,对函数 随自变量 的变化而变化的规律进行了探究.
下面是小涛的探究过程,请补充完整.
(1)列表:下表的已知数据是 , 两点间的距离 进行取点、画图、测量,分别得到了 与 的几组对应值:
|
0 |
0.30 |
0.50 |
1.00 |
1.50 |
2.00 |
2.50 |
|
3.00 |
3.50 |
3.68 |
3.81 |
3.90 |
3.93 |
4.10 |
|
|
2.88 |
2.81 |
2.69 |
2.67 |
2.80 |
3.15 |
|
3.85 |
5.24 |
6.01 |
6.71 |
7.27 |
7.44 |
8.87 |
请你通过计算,补全表格;
(2)描点、连线,在平面直角坐标系 中,描出表格中各组数值所对应的点 ,并画出函数 关于 的图象.

(3)探究性质:随着自变量 的不断增大,函数 的变化趋势: .
(4)解决问题:当 时, 的长度大约是 .(保留两位小数).
如图,是
与弦
所围成的图形的外部的一定点,
是
上一动点,连接
交弦
于点
.
小腾根据学习函数的经验,对线段,
,
的长度之间的关系进行了探究.下面是小腾的探究过程,请补充完整:
(1)对于点在
上的不同位置,画图、测量,得到了线段
,
,
的长度的几组值,如下表:
位置1 |
位置2 |
位置3 |
位置4 |
位置5 |
位置6 |
位置7 |
位置8 |
|
3.44 |
3.30 |
3.07 |
2.70 |
2.25 |
2.25 |
2.64 |
2.83 |
|
3.44 |
2.69 |
2.00 |
1.36 |
0.96 |
1.13 |
2.00 |
2.83 |
|
0.00 |
0.78 |
1.54 |
2.30 |
3.01 |
4.00 |
5.11 |
6.00 |
在,
,
的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:当时,
的长度约为
.
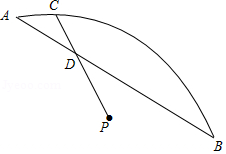
如图,是
与弦
所围成的图形的内部的一定点,
是弦
上一动点,连接
并延长交
于点
,连接
.已知
,设
,
两点间的距离为
,
,
两点间的距离为
,
,
两点间的距离为
.
小腾根据学习函数的经验,分别对函数,
随自变量
的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量的值进行取点、画图、测量,分别得到了
,
与
的几组对应值;
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
5.62 |
4.67 |
3.76 |
|
2.65 |
3.18 |
4.37 |
|
5.62 |
5.59 |
5.53 |
5.42 |
5.19 |
4.73 |
4.11 |
(2)在同一平面直角坐标系中,描出补全后的表中各组数值所对应的点
,
,并画出函数
,
的图象;

(3)结合函数图象,解决问题:当为等腰三角形时,
的长度约为
.
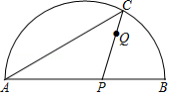
如图,是
所对弦
上一动点,过点
作
交
于点
,连接
,过点
作
于点
.已知
,设
、
两点间的距离为
,
、
两点间的距离为
.(当点
与点
或点
重合时,
的值为
小东根据学习函数的经验,对函数随自变量
的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了与
的几组值,如下表:
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
0 |
2.0 |
2.3 |
2.1 |
|
0.9 |
0 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出已补全后的表中各对对应值为坐标的点,画出该函数的图象.
(3)结合画出的函数图象,解决问题:当为等腰三角形时,
的长度约为
.