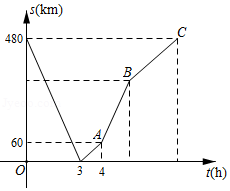
甲、乙两地相距 ,一辆汽车上午 从甲地出发驶往乙地,匀速行驶了一半的路程后将速度提高了 ,并继续匀速行驶至乙地,汽车行驶的路程 与时间 之间的函数关系如图所示,该车到达乙地的时间是当天上午

A. B. C. D.
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,两车在途中相遇时,快车恰巧出现故障,慢车继续驶往甲地,快车维修好后按原速继续行驶乙地,两车到达各地终点后停止,两车之间的距离 与慢车行驶的时间 之间的关系如图:
(1)快车的速度为 , 点的坐标为 .
(2)慢车出发多少小时后,两车相距 .
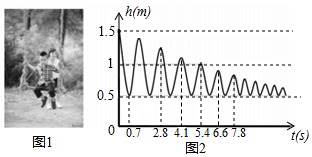
小红帮弟弟荡秋千(如图 ,秋千离地面的高度 与摆动时间 之间的关系如图2所示.
(1)根据函数的定义,请判断变量 是否为关于 的函数?
(2)结合图象回答:
①当 时, 的值是多少?并说明它的实际意义.
②秋千摆动第一个来回需多少时间?
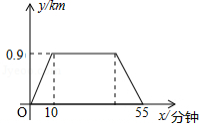
小明从家到图书馆看报然后返回,他离家的距离 与离家的时间 之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为 .
均匀地向一个容器注水,最后把容器注满,在注水过程中,水面高度 随时间 的变化规律如图所示(图中 为折线),这个容器的形状可以是

A. B.
B.
C. D.
D.
小明从家出发沿笔直的公路去图书馆,在图书馆阅读书报后按原路回到家.如图,反映了小明离家的距离 (单位: 与时间 (单位: 之间的对应关系.下列描述错误的是

| A. |
小明家距图书馆 |
| B. |
小明在图书馆阅读时间为 |
| C. |
小明在图书馆阅读书报和往返总时间不足 |
| D. |
小明去图书馆的速度比回家时的速度快 |
已知圆锥的侧面积是 ,若圆锥底面半径为 ,母线长为 ,则 关于 的函数图象大致是
A. B.
B.
C.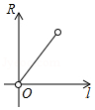 D.
D.
规定: 表示不大于 的最大整数, 表示不小于 的最小整数, 表示最接近 的整数 , 为整数),例如: , , .则下列说法正确的是 .(写出所有正确说法的序号)
①当 时, ;
②当 时, ;
③方程 的解为 ;
④当 时,函数 的图象与正比例函数 的图象有两个交点.
一对变量满足如图的函数关系.设计以下问题情境:
①小明从家骑车以600米 分的速度匀速骑了2.5分钟,在原地停留了2分钟,然后以1000米 分的速度匀速骑回家.设所用时间为 分钟,离家的距离为 千米;
②有一个容积为1.5升的开口空瓶,小张以0.6升 秒的速度匀速向这个空瓶注水,注满后停止,等2秒后,再以1升 秒的速度匀速倒空瓶中的水.设所用时间为 秒,瓶内水的体积为 升;
③在矩形 中, , ,点 从点 出发.沿 路线运动至点 停止.设点 的运动路程为 , 的面积为 .
其中,符合图中函数关系的情境个数为

| A. |
3 |
B. |
2 |
C. |
1 |
D. |
0 |
如图,在物理课上,小明用弹簧秤将铁块 悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧秤的读数 (单位: 与铁块被提起的高度 (单位: 之间的函数关系的大致图象是

A. B.
B.
C. D.
D.
小明和小华是同班同学,也是邻居,某日早晨,小明 先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公交汽车到了学校.如图是他们从家到学校已走的路程 (米 和所用时间 (分钟)的关系图.则下列说法中错误的是

A.小明吃早餐用时5分钟
B.小华到学校的平均速度是240米 分
C.小明跑步的平均速度是100米 分
D.小华到学校的时间是
甲、乙两车从 地出发,匀速驶向 地.甲车以 的速度行驶 后,乙车才沿相同路线行驶.乙车先到达 地并停留 后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离 与乙车行驶时间 之间的函数关系如图所示.下列说法:①乙车的速度是 ;② ;③点 的坐标是 ;④ .其中说法正确的有

A.4个B.3个C.2个D.1个
下面哪幅图,可以大致刻画出苹果成熟后从树上下落过程中(落地前),速度变化的情况
A. B.
B.
C. D.
D.