初中数学函数关系式试题

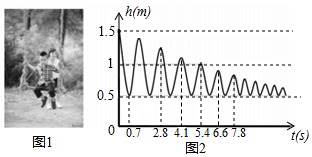
小红帮弟弟荡秋千（如图 $1)$，秋千离地面的高度 $ℎ\left(m\right)$与摆动时间 $t\left(s\right)$之间的关系如图2所示．

（1）根据函数的定义，请判断变量 $ℎ$是否为关于 $t$的函数？

（2）结合图象回答：

①当 $t=0.7s$时， $ℎ$的值是多少？并说明它的实际意义．

②秋千摆动第一个来回需多少时间？

某个函数具有性质：当 $x>0$时， $y$随 $x$的增大而增大，这个函数的表达式可以是　             　（只要写出一个符合题意的答案即可）．

对任意实数 $a$， $b$定义运算“ $\varnothing$”： $\mathit{a\varnothing b}=\left\{\begin{array}{c}a(a>b)\\ b(a⩽b)\end{array}\right.$，则函数 $y=x^2\varnothing (2-x)$的最小值是 $($　　 $)$

A． $-1$B．0C．1D．4

如图，四边形 $\mathit{ABCD}$为一个矩形纸片， $\mathit{AB}=3$， $\mathit{BC}=2$，动点 $P$自 $D$点出发沿 $\mathit{DC}$方向运动至 $C$点后停止， $\mathit{\Delta ADP}$以直线 $\mathit{AP}$为轴翻折，点 $D$落在点 $D_1$的位置．设 $\mathit{DP}=x$，△ $A{D}_{1}P$与原纸片重叠部分的面积为 $y$．

（1）当 $x$为何值时，直线 $A{D}_1$过点 $C$？

（2）当 $x$为何值时，直线 $A{D}_1$过 $\mathit{BC}$的中点 $E$？

（3）求出 $y$与 $x$的函数表达式．

同一温度的华氏度数 $y{(}^{°}\text{F})$与摄氏度数 $x{(}^{°}\text{C})$之间的函数表达式是 $y=\frac{9}{5}x+32$．若某一温度的摄氏度数值与华氏度数值恰好相等，则此温度的摄氏度数为　    　 ${}^{°}\text{C}$．

如图，矩形 $\mathit{ABCD}$ 中， $\mathit{AB}=6$ ， $\mathit{AD}=8$ ，点 $E$ 在边 $\mathit{AD}$ 上， $\mathit{CE}$ 与 $\mathit{BD}$ 相交于点 $F$ ．设 $\mathit{DE}=x$ ， $\mathit{BF}=y$ ，当 $0⩽x⩽8$ 时， $y$ 关于 $x$ 的函数解析式为 　　．

如图，在矩形 $\mathit{ABCD}$ 中， $\mathit{AB}=2$ ， $\mathit{AD}=1$ ，点 $E$ 为边 $\mathit{CD}$ 上的一点（与 $C$ 、 $D$ 不重合），四边形 $\mathit{ABCE}$ 关于直线 $\mathit{AE}$ 的对称图形为四边形 $\mathit{ANME}$ ，延长 $\mathit{ME}$ 交 $\mathit{AB}$ 于点 $P$ ，记四边形 $\mathit{PADE}$ 的面积为 $S$ ．

（1）若 $\mathit{DE}=\frac{\sqrt{3}}{3}$ ，求 $S$ 的值；

（2）设 $\mathit{DE}=x$ ，求 $S$ 关于 $x$ 的函数表达式．

阅读下面的材料：

如果函数满足：对于自变量的取值范围内的任意，，

（1）若，都有，则称是增函数；

（2）若，都有，则称是减函数．

例题：证明函数是减函数．

证明：设，

．

，

，．

．即．

．

函数是减函数．

根据以上材料，解答下面的问题：

已知函数，

，

（1）计算：　　，　　；

（2）猜想：函数是　　函数（填“增”或“减” ；

（3）请仿照例题证明你的猜想．

某函数满足当自变量时，函数值，当自变量时，函数值，写出一个满足条件的函数表达式　 　．