如图,在平面直角坐标系中,将边长为1的正六边形 绕点 顺时针旋转 个 ,得到正六边形 ,则正六边形 的顶点 的坐标是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在单位长度为1米的平面直角坐标系中,曲线是由半径为2米,圆心角为 的 多次复制并首尾连接而成.现有一点 从 为坐标原点)出发,以每秒 米的速度沿曲线向右运动,则在第2019秒时点 的纵坐标为

| A. |
|
B. |
|
C. |
0 |
D. |
1 |
如图,在平面直角坐标系中,将正方形 绕点 逆时针旋转 后得到正方形 ,依此方式,绕点 连续旋转2018次得到正方形 ,如果点 的坐标为 ,那么点 的坐标为

A. B. C. D.
在平面直角坐标系中,一个智能机器人接到如下指令:从原点 O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1 m.其行走路线如图所示,第1次移动到 A 1,第2次移动到 A 2,…,第 n次移动到 A n.则△ OA 2 A 2018的面积是( )

| A. |
504m 2 |
B. |
m 2 |
C. |
m 2 |
D. |
1009m 2 |
在平面直角坐标系中,一个智能机器人接到的指令是:从原点 出发,按"向上 向右 向下 向右"的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点 ,第二次移动到点 第 次移动到点 ,则点 的坐标是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在平面直角坐标系中,将 沿 轴向右滚动到△ 的位置,再到△ 的位置 依次进行下去,若已知点 , ,则点 的坐标为

A. B. C. D.
如图,点 , , 在反比例函数 的图象上,点 , , , 在 轴上,且 ,直线 与双曲线 交于点 , , , ,则 为正整数)的坐标是

| A. |
, |
B. |
|
C. |
, |
D. |
, |
我们把1,1,2,3,5,8,13,21, 这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作 圆弧 , , , 得到斐波那契螺旋线,然后顺次连接 , , , 得到螺旋折线(如图),已知点 , , ,则该折线上的点 的坐标为
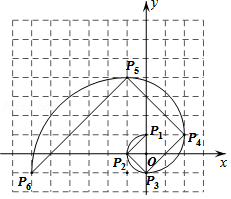
A. B. C. D.
如图,在单位为1的方格纸上,△ ,△ ,△ , ,都是斜边在 轴上,斜边长分别为2,4,6, 的等腰直角三角形,若△ 的顶点坐标分别为 , , ,则依图中所示规律, 的坐标为

| A. |
|
B. |
|
C. |
|
D. |
|
一组正方形按如图所示的方式放置,其中顶点 在 轴上,顶点 、 、 、 、 、 、 在 轴上,已知正方形 的边长为1, , 则正方形 的边长是

A. B. C. D.
如图,过点 作直线
作直线 的垂线,垂足为点
的垂线,垂足为点 ,过点
,过点 作
作 轴,垂足为点
轴,垂足为点 ,过点
,过点 作
作 ,垂足为点
,垂足为点 ,
, ,这样依次下去,得到一组线段:
,这样依次下去,得到一组线段: ,
, ,
, ,
, ,则线段
,则线段 的长为
的长为


A. B.
B. C.
C. D.
D.
如图,在平面直角坐标系中,直线 与直线 交于点 ,过 作 轴的垂线,垂足为 ,过 作 的平行线交 于 ,过 作 轴的垂线,垂足为 ,过 作 的平行线交 于 ,过 作 轴的垂线,垂足为 按此规律,则点 的纵坐标为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在平面直角坐标系中, , , .先将四边形ABCD沿x轴翻折,再向右平移8个单位长度,向下平移1个单位长度后,得到四边形A1B1C1D1,最后将四边形A1B1C1D1,绕着点A1旋转,使旋转后的四边形对角线的交点落在x轴上,则旋转后的四边形对角线的交点坐标为( )

A.(4,0)B.(5,0)
C.(4,0)或(﹣4,0)D.(5,0)或(﹣5,0)
如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),动点P从点A出发,以每秒2个单位的速度按逆时针方向沿四边形ABCD的边做环绕运动;另一动点Q从点C出发,以每秒3个单位的速度按顺时针方向沿四边形CBAD的边做环绕运动,则第2014次相遇点的坐标是( )

| A.(﹣1,﹣1) | B.(﹣1,1) | C.(﹣2,2) | D.(1,2) |