初中数学一元二次方程选择题

关于 $x$ 的方程 $x^2+2(m-1)x+m^2-m=0$ 有两个实数根 $\alpha$ ， $\beta$ ，且 ${\alpha }^2+{\beta }^2=12$ ，那么 $m$ 的值为 $($ 　　 $)$

A．

$-1$

B．

$-4$

C．

$-4$ 或1

D．

$-1$ 或4

将关于 $x$ 的一元二次方程 $x^2-\mathit{px}+q=0$ 变形为 $x^2=\mathit{px}-q$ ，就可以将 $x^2$ 表示为关于 $x$ 的一次多项式，从而达到"降次"的目的，又如 $x^3=x·x^2=x(\mathit{px}-q)=\dots$ ，我们将这种方法称为"降次法"，通过这种方法可以化简次数较高的代数式．根据"降次法"，已知： $x^2-x-1=0$ ，且 $x>0$ ，则 $x^4-2x^3+3x$ 的值为 $($ 　　 $)$

A．

$1-\sqrt{5}$

B．

$3-\sqrt{5}$

C．

$1+\sqrt{5}$

D．

$3+\sqrt[]{5}$

定义新运算" $a*b$ "：对于任意实数 $a$ ， $b$ ，都有 $a*b=(a+b)(a-b)-1$ ，其中等式右边是通常的加法、减法、乘法运算，例 $4*3=(4+3)(4-3)-1=7-1=6$ ．若 $x*k=x(k$ 为实数）是关于 $x$ 的方程，则它的根的情况为 $($ 　　 $)$

A．	有一个实数根	B．	有两个相等的实数根
C．	有两个不相等的实数根	D．	没有实数根

若抛物线 $y=a{x}^2+\mathit{bx}+c(a>0)$ 经过第四象限的点 $(1,-1)$ ，则关于 $x$ 的方程 $a{x}^2+\mathit{bx}+c=0$ 的根的情况是 $($ 　　 $)$

A．	有两个大于1的不相等实数根
B．	有两个小于1的不相等实数根
C．	有一个大于1另一个小于1的实数根
D．	没有实数根

目前以 $5G$ 等为代表的战略性新兴产业蓬勃发展．某市2019年底有 $5G$ 用户2万户，计划到2021年底全市 $5G$ 用户数累计达到8.72万户．设全市 $5G$ 用户数年平均增长率为 $x$ ，则 $x$ 值为 $($ 　　 $)$

A．

$20\%$

B．

$30\%$

C．

$40\%$

D．

$50\%$

如图，把一块长为 $40\mathit{cm}$ ，宽为 $30\mathit{cm}$ 的矩形硬纸板的四角剪去四个相同小正方形，然后把纸板的四边沿虚线折起，并用胶带粘好，即可做成一个无盖纸盒．若该无盖纸盒的底面积为 $600c{m}^2$ ，设剪去小正方形的边长为 $\mathit{xcm}$ ，则可列方程为 $($ 　　 $)$

A．	$(30-2x)(40-x)=600$	B．	$(30-x)(40-x)=600$
C．	$(30-x)(40-2x)=600$	D．	$(30-2x)(40-2x)=600$

已知 $x_1$ ， $x_2$ 是方程 $x^2-3x-2=0$ 的两根，则 $x_1^2+x_2^2$ 的值为 $($ 　　 $)$

A．

5

B．

10

C．

11

D．

13

已知 $m$ 、 $n$ 、4分别是等腰三角形（非等边三角形）三边的长，且 $m$ 、 $n$ 是关于 $x$ 的一元二次方程 $x^2-6x+k+2=0$ 的两个根，则 $k$ 的值等于 $($ 　　 $)$

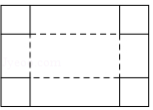
A．

7

B．

7或6

C．

6或 $-7$

D．

6

若菱形 $\mathit{ABCD}$ 的一条对角线长为8，边 $\mathit{CD}$ 的长是方程 $x^2-10x+24=0$ 的一个根，则该菱形 $\mathit{ABCD}$ 的周长为 $($ 　　 $)$

A．

16

B．

24

C．

16或24

D．

48

已知关于 $x$ 的一元二次方程 $x^2+5x-m=0$ 的一个根是2，则另一个根是 $($ 　　 $)$

A．

$-7$

B．

7

C．

3

D．

$-3$

已知关于 $x$ 的一元二次方程 $x^2-(2k+1)x+k^2+2k=0$ 有两个实数根 $x_1$ ， $x_2$ ，则实数 $k$ 的取值范围是 $($ 　　 $)$

A．

$k<\frac{1}{4}$

B．

$k⩽\frac{1}{4}$

C．

$k>4$

D．

$k⩽\frac{1}{4}$ 且 $k\ne 0$

已知关于 $x$ 的一元二次方程 $(m-1)x^2+2x+1=0$ 有实数根，则 $m$ 的取值范围是 $($ 　　 $)$

A．

$m<2$

B．

$m⩽2$

C．

$m<2$ 且 $m\ne 1$

D．

$m⩽2$ 且 $m\ne 1$

一元二次方程 $x^2-2x+1=0$ 的根的情况是 $($ 　　 $)$

A．	有两个不等的实数根	B．	有两个相等的实数根
C．	无实数根	D．	无法确定

某年级举办篮球友谊赛，参赛的每两个队之间都要比赛一场，共要比赛36场，则参加此次比赛的球队数是 $($ 　　 $)$

A．

6

B．

7

C．

8

D．

9

参加足球联赛的每两支球队之间都要进行两场比赛，共要比赛110场，设参加比赛的球队有 $x$ 支，根据题意，下面列出的方程正确的是 $($ 　　 $)$

A．

$\frac{1}{2}x(x+1)=110$

B．

$\frac{1}{2}x(x-1)=110$

C．

$x(x+1)=110$

D．

$x(x-1)=110$