观察下列等式：
第1 个等式：
；
第2个等式：
；
第3个等式：
；
第4个等式：
；
……
请解答下列问题：
（1）按以上规律列出第5个等式：
=_______=_________；
（2）用含有n的代数式表示第n个等式：
=_________=__________（n为正整数）；
（3）求
．
（本题6分）某校图书馆上周借书记录（超过100册的部分记为正，少于100册的部分记为负）如下表：
| 星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
| ＋18 |
－6 |
＋15 |
0 |
－12 |
（1）上星期五借出多少册书？
（2）上星期借书最多的一天比借书最少的一天多借出图书多少册？
（3）上星期平均每天借出多少册书？
列式计算：
已知下列各数：
， 6 ，
，0，
，写出整数的和与分数的积的差
某班抽查了10名同学的期末成绩，以80分为基准，超出的记为正数，不足的记为负数，记录的结果如下：
＋8，－3，＋12，－7，－10，－3，－8，＋1，0，＋10．
（1）这10名同学中最高分是多少？最低分是多少？
（2）10名同学的平均成绩是多少？
请阅读下列材料：让我们来规定一种运算：
，例如：
=2×5－3×4=10－12=－2. 按照这种运算的规定，若
=
，试用方程的知识求x的值。
运动会前夕，为了提高体能，小明每天放学回家做仰卧起坐．他制作
了一张表格记录自己每天做仰卧起坐的成绩．以每分钟做40个为标准，超过的个数记为正，不足的个数记为负．下表是小明一周做仰卧起坐的记录：
| 时间 |
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
星期六 |
星期日 |
| 个数 |
+14 |
+8 |
-5 |
+2 |
-10 |
+1 |
-3 |
根据上述记录表，回答下列问题：
（1）小明这周一天最多做 个，最少做 个；
（2）这周小明平均每天做多少个？
（本题6分）根据某地实验测得的数据表明，高度每增加1 km，气温大约下降6℃，已知该地地面温度为21℃．
（1）高空某处高度是8 km，求此处的温度是多少；
（2）高空某处温度为一24 ℃，求此处的高度．
探索性问题：
已知：b是最小的正整数，且a、b满足（c-5）2+|a+b|=0，请回答问题：
（1）请直接写出a、b、c的值．a= ，b= ，c= ；
（2）数轴上a、b、c三个数所对应的点分别为A、B、C，点A、B、C同时开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动，假设t秒钟过后，若点B与点C之间的距离表示为BC，点A与点B之间的距离表示为AB，点A与点C之间的距离表示为AC．
①t秒钟过后，AC的长度为 （用t的关系式表示）；
②请问：BC-AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．
计算下列各题：
（1）（+4．3）-（-4）+（-2．3）-（+4）；
（2）（-48）÷（-2）3-（-25）×（-4）+（-2）2；
（3）（-1．5）×3×（-
）2-（-
）×（-1．5）2
（4）[（-
）3×（-
）2÷（-
）-32-（-3）3]×（-14）
把下列各数：-2．5，（-1）2，0，-|-2|，-（-3）在数轴上表示出来，并用“＜”把它们连接起来．
基本事实：若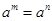
（a>0且a≠1，m、n是正整数），则m＝n．
试利用上述基本事实分别求下列各等式中x的值：
①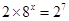
； ②
．
）+2．75－（+7
）
粤公网安备 44130202000953号