某文具店三月份销售铅笔100支,四、五两个月销售量连续增长.若月平均增长率为 ,则该文具店五月份销售铅笔的支数是
A. B. C. D.
某市出租车收费标准是:起步价10元,可乘3千米;3千米到5千米,每千米1.3元;超过5千米,每千米2.4元。
(1)若某人乘坐了 (
(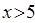 )千米的路程,则他应支付的费用是多少?
)千米的路程,则他应支付的费用是多少?
(2)若某人乘坐的路程为6千米,那么他应支付的费用是多少?
对任意一个四位数,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称
为“极数”.
(1)请任意写出三个“极数”;并猜想任意一个“极数”是否是99的倍数,请说明理由;
(2)如果一个正整数是另一个正整数
的平方,则称正整数
是完全平方数.若四位数
为“极数”,记
,求满足
是完全平方数的所有
.
观察下列一组数:,
,它们是按一定规律排列的,那么这组数的第
个数可用含
的式子表示为 .
为了节约用水,某市规定三口之家每月标准用水量为15立方米,超过部分加价收费,假设不超过部分水费为1.5元/立方米,超过部分水费为3元/立方米。
(1)当每月用水量为a立方米时,请用代数式分别表示这家按标准用水量和超出标准用水时各应缴纳的水费;
(2)如果甲、乙两家用水量分别为10立方米和20立方米,那么甲、乙两家该月应各交多少水费?
(3)当丁家本月交水费46.5元时,那么丁家该月用水多少立方米?
礼堂第一排有m个座位,后面每排比前一排多一个座位,则第n排的座位个数有( )
| A.m+n |
| B.mn+1 |
| C.m+(n-1) |
| D.n+(n+1) |
规律探究.下面有8个算式,排成4行2列
2+2, 2×2
3+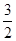 , 3×
, 3×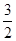
4+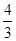 , 4×
, 4×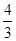
5+ , 5×
, 5× ……, ……
……, ……
(1)同一行中两个算式的结果怎样?
(2)算式2005+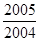 和2005×
和2005×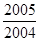 的结果相等吗?
的结果相等吗?
(3)请你试写出算式,试一试,再探索其规律,并用含自然数n的代数式表示这一规律.
某地居民生活用水收费标准:每月用水量不超过17立方米,每立方米 元;超过部分每立方米 元.该地区某用户上月用水量为20立方米,则应缴水费为
| A. |
元 |
B. |
元 |
C. |
元 |
D. |
元 |
“绿水青山就是金山银山”,为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向 , 两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥; , 两个果园分别需用110吨和70吨有机化肥.两个仓库到 , 两个果园的路程如表所示:
路程(千米) |
||
甲仓库 |
乙仓库 |
|
果园 |
15 |
25 |
果园 |
20 |
20 |
设甲仓库运往 果园 吨有机化肥,若汽车每吨每千米的运费为2元,
(1)根据题意,填写下表.
运量(吨 |
运费(元 |
|||
甲仓库 |
乙仓库 |
甲仓库 |
乙仓库 |
|
果园 |
|
|
|
|
果园 |
|
|
|
|
(2)设总运费为 元,求 关于 的函数表达式,并求当甲仓库运往 果园多少吨有机化肥时,总运费最省?最省的总运费是多少元?