初中数学计算器—基础知识试题

一只甲虫在5×5的方格（每小格边长为1m）上沿着网格线运动。它从A处出发去看望B、C、D处的其它甲虫（A,B,C,D都在格点上）。规定：向上向右走为正，向下向左走为负。如果从A到B记为：A→B（＋1，＋4），从B到A记为：A→B（－1，－4），其中第一个数表示左右方向，第二个数表示上下方向，那么图中

（1）A→C（    ，    ），B→C（    ，    ）,C→     （＋1，    ）；
（2）若这只甲虫的行走路线为A→D→C→B，请计算该甲虫走过的路程；
（3）若这只甲虫从A处去甲虫P处的行走路线依次为（＋2，＋1），（＋3，2），（－2，-1），（－1，－2），请在图中标出P的位置。
(4) 在(3)中甲虫若每走1m需消耗1.5焦耳的能量,则甲虫从A走到P的过程中共需消耗多少焦耳的能量?  

若一次函数的图像与坐标轴的两个交点的距离是5，则k的值为     .

如图，直线，点坐标为（1，0），过点作轴的垂线交直线于点B，以原点O为圆心，长为半径画弧交轴于点；再过点作的垂线交直线于点，以原点O为圆心，长为半径画弧交轴于点，…，按此做法进行下去，点的坐标为(   )．

A．

B．

C．

D．

已知抛物线的图象如图所示，则下列结论：①＞0；
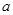②； ③＜； ④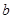＞1.其中正确的结论是 （  ）

A．①②

B．②③

C．③④

D．②④

如图，矩形OABC的长OA为2,宽AB为1，则该矩形绕点O逆时 针旋90^O后，B点的坐标为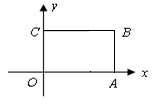

如图，梯形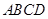中，为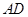中点,AB="2cm,BC=2cm," CD=0.5cm点在梯形的边上沿运动，速度为1cm/s，则的面积与点经过的路程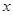cm之间的函数关系用图象表示大致是下图中的(      )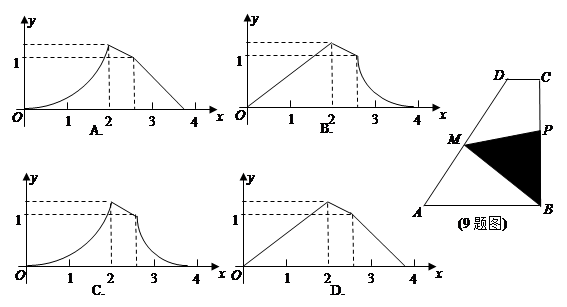

如图，已知抛物线经过O(0,0)，A(4,0),B(3,)三点，连接AB，过点B作BC∥轴交该抛物线于点C.

求这条抛物线的函数关系式.
两个动点P、Q分别从O、A同时出发,以每秒1个单位长度的速度运动. 其中，点P沿着线段0A向A点运动，点Q沿着线段AB向B点运动. 设这两个动点运动的时间为（秒) (0＜≤2)，△PQA的面积记为S.
① 求S与的函数关系式；
② 当为何值时，S有最大值，最大值是多少？并指出此时△PQA的形状；
是否存在这样的值，使得△PQA是直角三角形?若存在，请直接写出此时P、Q两点的坐标；若不存在，请说明理由.

近年来，我国煤矿安全事故频频发生，其中危害最大的是瓦斯，其主要成分是CO.在一次矿难事件的调查中发现：从零时起，井内空气中CO的浓度达到4 mg/L，此后浓度成直线型增加，在第7小时达到最高值46 mg/L，发生爆炸；爆炸后，空气中的CO浓度成反比例下降.如图，根据题中相关信息回答下列问题：
（1）求爆炸前后空气中CO浓度y与时间x的函数关系式，并写出相应的自变量取值范围；
（2）当空气中的CO浓度达到34 mg/L时，井下3km的矿工接到自动报警信号，这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生？
（3）矿工只有在空气中的CO浓度降到4 mg/L及以下时，才能回到矿井开展生产自救，求矿工至少在爆炸后多少小时才能下井?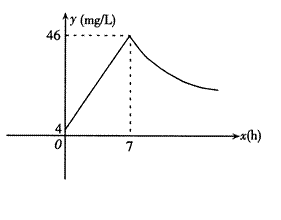

如图1是三个边长为2的正方形小方格，反比例函数经过正方形
格点D,与小方格交与点E、点F，直线EF的解析式为y="mx+a." 如图2所示的△ABC为Rt△，∠B=90°，AB=10厘米，BC=a厘米。
（1）求反比例函数的解析式。
（2）求一次函数的解析式。
（3）已知点P从点A出发沿AB边向点B以1厘米/秒的速度移动，点Q从点B出发沿BC边向点C以2厘米/秒的速度移动，如果P、Q两点同时出发，几秒种后，△BPQ的面积与是△ABC的面积一半？

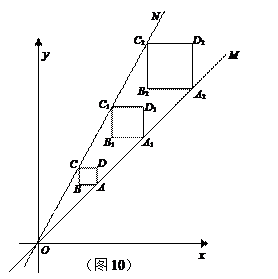
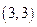（本题12分）如图10，正方形ABCD、正方形A₁B₁C₁D₁、正方形A₂B₂C₂D₂均位于第一象限内，它们的边平行于x轴或y轴，其中点A、A₁、A₂在直线OM上，点C、C₁、C₂在直线ON上，O为坐标原点，已知点A的坐标为，正方形ABCD的边长为1.
（1）求直线ON的表达式；
（2）若点C₁的横坐标为4，求正方形A₁B₁C₁D₁的边长；
（3）若正方形A₂B₂C₂D₂的边长为a，则点B₂的坐标为（　　）.　
（A）　　（B）　　（C）　　（D）

如图，在平面直角坐标系中，长、宽分别为2和1的矩形ABCD的边上有一动点
P，沿A→B→C→D→A运动一周，则点P的纵坐标y与P所走过的路程S之间的函数关系
用图象表示大致是【  】

函数的自变量x的取值范围是

A．

B．且

C．

D．且

（11·贺州）如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1
次从原点运动到点(1，1)，第2次接着运动到点(2，0)，第3次接着运动到点(3，2)，……，
按这样的运动规律，经过第2011次运动后，动点P的坐标是_  ▲  ．

（11·贺州）在数轴上表示－5的点到原点的距离是_  ▲  ．

若一次函数的图象经过反比例函数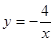图象上的两点（1，m）和（n，2），则这个一次函数的解析式是___________.