如图是某蓄水池的横断面示 意图,分为深水池和浅水池,如果这个蓄水池以固定的流量注水,下面图象中,能大致表示水的最大深度h与时间t之间的关系是( )
意图,分为深水池和浅水池,如果这个蓄水池以固定的流量注水,下面图象中,能大致表示水的最大深度h与时间t之间的关系是( )

小明的爸爸早晨出去散步,从家走了20分到达距离家800米的公园,他在公园休息了10分,然后用30分原路返回家中,那么小明的爸爸离家的距离S(单位:米)与离家的时间t(单位:分)之间的函数关系图象大致是( )
已知点P(a-1,a+2)在平面直角坐标系的第二象限内,则a的取值范围在数轴上可表示为(阴影部分)

如图是胡老师画的一幅写生画,四位同学对这幅画的作画时间作了猜测. 根据胡老师给出的方向坐标,猜测比较合理的是 ( )
| A.小明:“早上8点” | B.小亮:“中午12点” |
| C.小刚:“下午5点” | D.小红:“什么时间都行” |
如图,根据要求回答下列问题:
(1)点A关于y轴对称点A'的坐标是____________;
点B关于y轴对称点B'的坐标是______________;
点C关于y轴对称点C'的坐标是______________;
(2)作出与△ABC关于y轴对称的图形△A′B′C′(不要求写作法)
某医药研究所开发了一种新药,在试验药效时发现,假如成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克,接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y微克随时间x小时的变化如图所示,当成人按规定剂量服药后,
(1)分别求出 x≤2和 x≥2时,y 与x之间的函数关系式
(2)假如每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的,那么这个有效时间是多长?
如图,在矩形ABCD中,AB=4,BC=3,点P在CD边上运动,联结AP,过点B作BE⊥AP,垂足为E,设AP= ,BE=
,BE=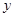 ,则能反映
,则能反映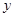 与
与 之间函数关系的图象大致是
之间函数关系的图象大致是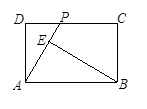
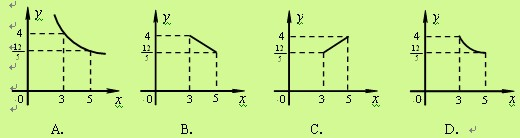
某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的余油量y(L)与工作时间x(h)之间为一次函数关系,如图所示.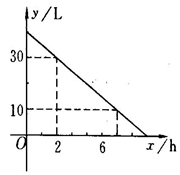
(1)求y与x的函数解析式.
(2)一箱油可供拖位机工作几小时?