小学数学约数个数与约数和定理试题

能被2145整除且恰有2145个约数的数有         个．

求满足条件的a、b的值(a、b都是四位数)．

在三位数中，恰好有9个约数的数有多少______个？

1001的倍数中，共有     个数恰有1001个约数．

设A共有9个不同的约数，B共有6个不同的约数，C共有8个不同的约数，这三个数中的任何两个都不整除，则这三个数之积的最小值是多少？

如果一个自然数的2004倍恰有2004个约数，这个自然数自己最少有多少个约数？

已知自然数A、B满足以下2个性质：（1）A、B不互质  （2）A、B的最大公约数与最小公倍数之和为35。那么A+B的最小值是多少？

有两个自然数，它们的和等于297，它们的最大公约数与最小公倍数之和等于693，这两个自然数的差是         ．

如图，A、B、C是三个顺次咬和的齿轮，当A转4圈时，B恰好转3圈：当B转4圈时，C恰好转5圈，则A、B、C的齿数的最小数分别是多少？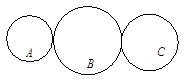     

已知偶数A不是4的整数倍，它的约数的个数为12，求4A的约数的个数.

两个整数A、B的最大公约数是C，最小公倍数是D，并且已知C不等于1，也不等于A或B，C+D=187，那么A+B等于多少？

有一串数：1，1，2，3，5，8，……，从第三个数起，每个数都是前两个数之和，在这串数的前2009个数中，有几个是5的倍数？

试说明一个5位数，原序数与反序数的差一定是99的倍数(如：12367为原序数，那么它对应的反序数为76321，它们的差是99的倍数．)

把40，44，45，63，65，78，99，105这八个数平分成两组，使每组四个数的乘积相等。

有3堆小石子，每次允许进行如下操作：从每堆中取走同样数目的小石子，或是将其中的某一石子数是偶数的堆中的一半石子移入另外的一堆．开始时，第一堆有1989块石子，第二堆有989块石子，第三堆有89块石子．问，能否做到：
⑴某2堆石子全部取光？
⑵3堆中的所有石子都被取走？