小学奥数数论专题——整除
整除1.173□是一个四位数.数学老师说:“我在其中的方框内中先后填入3个数字,所得到的3个四位数:依次可被9,1l,6整除.”问:数学老师先后填入的3个数字的和是多少?
从0,1,2,3,4,5,6,7,8,9这10个数字中选出5个不同的数字组成一个五位数,使它能被3,5,7,13整除,这个数最大是多少?
将自然数1,2,3,…依次写下去组成一个数:12345678910111213….如果写到某个自然数时,所组成的数恰好第一次能被72整除,那么这个自然数是多少?
1~9九个数字按下图所示的次序排成一个圆圈,请在某两个数之间剪开,分别按顺时针和逆时针次序形成两个九位数.如果要求剪开后所得到的两个九位数的差能被396整除,那么应在何处剪开?
1至9这9个数字,按图所示的次序排成一个圆圈.请你在某两个数字之间剪开,分别按顺时针和逆时针次序形成两个九位数(例如,在l和7之间剪开,得到两个数是193426857和758624391).如果要求剪开后所得到的两个九位数的差能被396整除,那么剪开处左右两个数字的乘积是多少?
有15位同学,每位同学都有编号,他们是1号到15号.1号同学写了一个自然数,2号说:“这个数能被2整除”,3号说:“这个数能被3整除”,……,依次下去,每位同学都说,这个数能被他的编号数整除.1号作了一一验证:只有编号连续的两位同学说得不对,其余同学都对.问:
(1)说得不对的两位同学,他们的编号是哪两个连续自然数?
(2)如果告诉你,1号写的数是五位数,请求出这个数.
有20位同学,每位同学都有编号,他们是1号到20号.1号同学写了一个自然数,2号说:“这个数能被2整除”,3号说:“这个数能被3整除”,……,依次下去,每位同学都说,这个数能被他的编号数整除.1号作了一一验证:只有编号连续的两位同学说得不对,其余同学都对.问:
(1)说得不对的两位同学,他们的编号是哪两个连续自然数?
(2)如果告诉你,1号写的数是七位数,请求出这个数.
找出4个不同的自然数,使得对于其中任何两个数,它们的和总可以被它们的差整除.如果要求这4个数中最大的数与最小的数的和尽可能的小,那么这4个数里中间两个数的和是多少?
如图,依次排列的5个数是13,12,15,25,20.它们每相邻的两个数相乘得4个数.这4个数每相邻的两个数相乘得3个数.这3个数每相邻的两个数相乘得2个数.这2个数相乘得1个数.请问:最后这个数从个位起向左数,可以连续地数出几个零?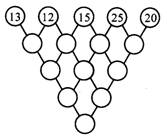
在方框中填上两个数字,可以相同也可以不同,使4□32□是9的倍数. ⑴请随便填出一种,并检查自己填的是否正确; ⑵一共有多少种满足条件的填法?
一位后勤人员买了72本笔记本,可是由于他吸烟不小心,火星落在帐本上,把这笔帐的总数烧去两个数字.帐本是这样的:72本笔记本,共□ □元(□为被烧掉的数字),请把□处数字补上,并求笔记本的单价.
□元(□为被烧掉的数字),请把□处数字补上,并求笔记本的单价.
张老师带领同学们去种树,学生的人数恰好等分成三组.已知老师和学生共种树312棵,老师与学生每人种的树一样多,并且不超过10棵.问:一共有多少学生?每人种了几棵树?
某班同学在班主任老师带领下去种树,学生恰好平均分成三组,如果老师与学生每人种树一样多,共种了1073棵,那么平均每人种了棵树?
某个自然数既能写成9个连续自然数的和,还同时可以写成10个连续自然数的和,也能写成11个连续自然数的和,那么这样的自然数最小可以是几?
有些数既能表示成3个连续自然数的和,又能表示成4个连续自然数的和;还能表示成5个连续自然数的和.请你找出700至1000之间,所有满足上述要求的数,并简述理由.
一个十位数,如果各位上的数字都不相同,那么就称为“十全数”,例如,3785942160就是一个十全数.现已知一个十全数能被1,2,3,…,18整除,并且它的前四位数是4876,那么这个十全数是多少?
把若干个自然数1、2、3、……连乘到一起,如果已知这个乘积的最末53位恰好都是零,那么最后出现的自然数最小应该是多少?最大是多少?
从左向右编号为1至1991号的1991名同学排成一行.从左向右1至11报数,报数为11的同学原地不动,其余同学出列;然后留下的同学再从左向右1至11报数,报数为11的同学留下,其余的同学出列;留下的同学第三次从左向右1至1l报数,报到11的同学留下,其余同学出列.那么最后留下的同学中,从左边数第一个人的最初编号是多少?
为了打开银箱,需要先输入密码,密码由7个数字组成,它们不是1、2就是3.在密码中1的数目比2多,2的数目比3多,而且密码能被3和16所整除.试问密码是多少?
为了打开银箱,需要先输入密码,密码由7个数字组成,它们不是2就是3.在密码中2的数目比3多,而且密码能被3和4所整除.试求出这个密码.
三位数的百位、十位和个位的数字分别是5,a和b,将它连续重复写2008次成为: .如果此数能被91整除,那么这个三位数
.如果此数能被91整除,那么这个三位数 是多少?
是多少?
试说明一个4位数,原序数与反序数的和一定是11的倍数(如:1236为原序数,那么它对应的反序数为6321,它们的和7557是11的倍数.)
试说明一个5位数,原序数与反序数的差一定是99的倍数(如:12367为原序数,那么它对应的反序数为76321,它们的差 是99的倍数.)
是99的倍数.)
1至9这9个数字,按图所示的次序排成一个圆圈.请你在某两个数字之间剪开,分别按顺时针和逆时针次序形成两个九位数(例如,在1和7之间剪开,得到两个数是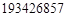 和
和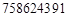 ).如果要求剪开后所得到的两个九位数的差能被
).如果要求剪开后所得到的两个九位数的差能被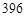 整除,那么剪开处左右两个数字的乘积是多少?
整除,那么剪开处左右两个数字的乘积是多少?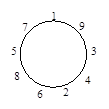
一个4位数,把它的千位数字移到右端构成一个新的4位数.已知这两个4位数的和是以下5个数的一个:①9865;②9866;③9867;④9868;⑤9869.这两个4位数的和到底是多少?
一个4位数,把它的千位数字移到右端构成一个新的4位数.再将新的4位数的千位数字移到右端构成一个更新的四位数,已知最新的4位数与最原先的4位数的和是以下5个数的一个:①9865;②9867;③9462;④9696;⑤9869.这两个4位数的和到底是多少?
有15位同学,每位同学都有编号,他们是1号到15号,1号同学写了一个自然数,其余各位同学都说这个数能被自己的编号数整除.1号作了检验:只有编号连续的两位同学说的不对,其余同学都对,问:⑴说的不对的两位同学,他们的编号是哪两个连续自然数?⑵如果告诉你1号写的数是五位数,请找出这个数.
某住宅区有12家住户,他们的门牌号分别是1,2,…,12.他们的电话号码依次是12个连续的六位自然数,并且每家的电话号码都能被这家的门牌号整除,已知这些电话号码的首位数字都小于6,并且门牌号是9的这一家的电话号码也能被13整除,问:这一家的电话号码是什么数?
 能被99整除,
能被99整除, 是多少?
是多少? 既是9的倍数,又是11的倍数;那么,这个九位数是多少?
既是9的倍数,又是11的倍数;那么,这个九位数是多少? 能被36整除,而且所得的商最小,那么
能被36整除,而且所得的商最小,那么 分别是多少?
分别是多少? 是一个三位数.它的百位数字是4,
是一个三位数.它的百位数字是4, 能被7整除,
能被7整除, 能被9整除,问
能被9整除,问 为例,说明被7、11、13整除的规律.
为例,说明被7、11、13整除的规律. 与
与 的和
的和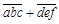 能被37整除,试说明:六位数
能被37整除,试说明:六位数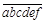 也能被37整除.
也能被37整除. 能被6整除,那么
能被6整除,那么 也能被6整除.
也能被6整除. ,试问
,试问 能否被8整除?请说明理由.
能否被8整除?请说明理由. 和
和 相乘,要使它们的乘积能被72整除,求
相乘,要使它们的乘积能被72整除,求 和
和 .
. 能被15整除,则
能被15整除,则 代表的数字是多少?
代表的数字是多少? 能被13整除,求О内的数字.
能被13整除,求О内的数字. 可被7整除?
可被7整除? ,能被11整除,
,能被11整除, 最小值为多少?
最小值为多少? 能被11整除,那么,
能被11整除,那么, 的最小值为多少?
的最小值为多少? ,如果满足
,如果满足 ,则称
,则称 ,则
,则 就是“迎春数”).请你求出所有“迎春数”的总和.
就是“迎春数”).请你求出所有“迎春数”的总和. .则
.则 ?
? 的各位数字都不相同且全都不为0,并且二位数
的各位数字都不相同且全都不为0,并且二位数 可被2整除,三位数
可被2整除,三位数 可被3整除,四位数
可被3整除,四位数 可被4整除,……依此类推,九位数
可被4整除,……依此类推,九位数 粤公网安备 44130202000953号
粤公网安备 44130202000953号