小学奥数组合问题专题——构造与论证
一个盒子里有400枚棋子,其中黑色和白色的棋子各200枚.下面我们对这些棋子做如下操作:每次拿出2枚棋子,如果颜色相同,就补1枚黑色棋子回去;如果颜色不同,就补1枚白色的棋子回去.这样的操作,实际上就是每次都少了1枚棋子,那么,经过399次操作后,最后剩下的棋子是黑色还是白色?
5卷本百科全书按从第1卷到第5卷的递增序号排列,今要将它们变为反序排列,即从第5卷到第1卷.如果每次只能调换相邻的两卷,那么最少要调换多少次?
有3堆小石子,每次允许进行如下操作:从每堆中取走同样数目的小石子,或是将其中的某一石子数是偶数的堆中的一半石子移入另外的一堆.开始时,第一堆有1989块石子,第二堆有989块石子,第三堆有89块石子.问能否做到:
(1)某2堆石子全部取光? (2)3堆中的所有石子都被取走?
在某市举行的一次乒乓球邀请赛上,有3名专业选手与3名业余选手参加.比赛采用单循环方式进行,就是说每两名选手都要比赛一场.为公平起见,用以下方法记分:开赛前每位选手各有10分作为底分,每赛一场,胜者加分,负者扣分,每胜专业选手一场加2分,每胜业余选手一场加1分;专业选手每负一场扣2分,业余选手每负一场扣1分.问:一位业余选手最少要胜几场,才能确保他的得分比某位专业选手高?
n支足球队进行比赛,比赛采用单循环制,即每对均与其他各队比赛一场.现规定胜一场得2分,平一场得1分,负一场得0分.如果每一队至少胜一场,并且所有各队的积分都不相同,问:
(1)n=4是否可能?
(2)n=5是否可能?
如图,将1,2,3,4,5,6,7,8,9,10这10个数分别填入图中的10个圆圈内,使任意连续相邻的5个圆圈内的各数之和均不大于某个整数M.求M的最小值并完成你的填图.
如图,在时钟的表盘上任意作 个
个 的扇形,使得每一个扇形都恰好覆盖
的扇形,使得每一个扇形都恰好覆盖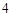 个数,且每两个扇形覆盖的数不全相同,求证:一定可以找到
个数,且每两个扇形覆盖的数不全相同,求证:一定可以找到 个扇形,恰好覆盖整个表盘上的数.并举一个反例说明,作
个扇形,恰好覆盖整个表盘上的数.并举一个反例说明,作 个扇形将不能保证上述结论成立.
个扇形将不能保证上述结论成立.
1998名运动员的号码依次为1至1998的自然数.现在要从中选出若干名运动员参加仪仗队,使得剩下的运动员中没有一个人的号码等于另外两人的号码的乘积.那么,选为仪仗队的运动员最少有多少人?
一组互不相同的自然数,其中最小的数是l,最大的数是25,除1之外,这组数中的任一个数或者等于这组数中某一个数的2倍,或者等于这组数中某两个数之和.问:这组数之和的最小值是多少?当取到最小值时,这组数是怎样构成的?
在下图中有16个黑点,它们排成了一个4×4的方阵.用线段连接其中4点,就可以画出各种不同的正方形.现在要去掉某些点,使得其中任意4点都不能连成正方形,那么最少要去掉多少个点?
某学校的学生中,没有一个学生读过学校图书馆的所有图书,又知道图书馆内任何两本书都至少被一个同学都读过.问:能否找到两个学生甲、乙和三本书4、B、C,使得甲读过A、B,没读过C,乙读过B、C,没读过A?说明判断过程.
有9位数学家,每人至多能讲3种语言,每3个人中至少有2个人有共通的语言.求证:在这些数学家中至少有3人能用同一种语言交谈。
在1000×1000的方格表中任意选取n个方格染为红色,都存在3个红色方格,它们的中心构成一个直角三角形的顶点.求n的最小值.
甲、乙、丙三个班人数相同,在班级之间举行象棋比赛.各班同学都按l,2,3,4,…依次编号.当两个班比赛时,具有相同编号的同学在同一台对垒.在甲、乙两班比赛时,有15台是男、女生对垒;在乙、丙班比赛时,有9台是男、女生对垒.试说明在甲、丙班比赛时,男、女生对垒的台数不会超过24.并指出在什么情况下,正好是24 ?
将15×15的正方形方格表的每个格涂上红色、蓝色或绿色.证明:至少可以找到两行,这两行中某一种颜色的格数相同.
在平面上有7个点,其中任意3个点都不在同一条直线上.如果在这7个点之字连结18条线段,那么这些线段最多能构成多少个三角形 ?
在9×9棋盘的每格中都有一只甲虫,根据信号它们同时沿着对角线各自爬到与原来所在格恰有一个公共顶点的邻格中,这样某些格中有若干只甲虫,而另一些格则空着.问空格数最少是多少?
若干台计算机联网,要求:
①任意两台之间最多用一条电缆连接;
②任意三台之间最多用两条电缆连接;
③两台计算机之间如果没有电缆连接,则必须有另一台计算机和它们都连接有电缆.若按此要求最少要用79条电缆.
问:(1)这些计算机的数量是多少台?
(2)这些计算机按要求联网,最多可以连多少条电缆?
在一个6×6的方格棋盘中,将若干个1×1的小方格染成红色.如果随意划掉3行3列,在剩下的小方格中必定有一个是红色的.那么最少要涂多少个方格?
如图,把正方体的6个表面剖分成9个相等的正方形.现用红、黄、蓝3种颜色去染这些小正方形,要求有公共边的正方形所染的颜色不同.那么染成红色的正方形的个数最多是多少个?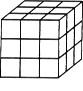
证明:在6×6×6的正方体盒子中最多可放入52个1×l×4的小长方体,这里每个小长方体的面都要与盒子的侧面平行.
用若干个l×6和1×7的小长方形既不重叠,也不留孔隙地拼成一个11×12的大长方形,最少要用小长方形多少个?
在黑板上写上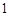 、
、 、
、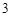 、
、 、……、
、……、 ,按下列规定进行“操怍”:每次擦去其中的任意两个数
,按下列规定进行“操怍”:每次擦去其中的任意两个数 和
和 ,然后写上它们的差(大数减小数),直到黑板上剩下一个数为止.问黑板上剩下的数是奇数还是偶数?为什么?
,然后写上它们的差(大数减小数),直到黑板上剩下一个数为止.问黑板上剩下的数是奇数还是偶数?为什么?
在1997×1997的正方形棋盘上的每格都装有一盏灯和一个按钮.按钮每按一次,与它同一行和同一列方格中的灯泡都改变一次状态,即由亮变为不亮,或由不亮变为亮.如果原来每盏灯都是不亮的,请说明最少需要按多少次按钮才可以使灯全部变亮?
在2009张卡片上分别写着数字1、2、3、4、……、2009,现在将卡片的顺序打乱,让空白面朝上,并在空白面上又分别写上1、2、3、4、……、2009.然后将每一张卡片正反两个面上的数字相加,再将这2009个和相乘,所得的积能否确定是奇数还是偶数?
将1、2、3、4、5、6写在一个圆周上,然后把圆周上连续三个数之和写下来,则可以得到六个数 、
、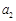 、
、 、
、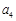 、
、 、
、 ,将这六个数中最大的记为
,将这六个数中最大的记为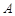 .请问在所有填写方式中,
.请问在所有填写方式中,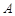 的最小值是什么?
的最小值是什么?
桌子上放着55根火柴,甲、乙二人轮流每次取走1~3根,规定谁取走最后一根火柴谁获胜.如果双方都采用最佳方法,甲先取,那么谁将获胜?
 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号