如图10-19所示，空中有水平向右的匀强电场和垂直于纸面向外的匀强磁场，质量为m，带电量为+q的滑块沿水平向右做匀速直线运动，滑块和水平面间的动摩擦因数为μ，滑块与墙碰撞后速度为原来的一半。滑块返回时，去掉了电场，恰好也做匀速直线运动，求原来电场强度的大小。
如图10-18所示，带电粒子在真空环境中的匀强磁场里按图示径迹运动。径迹为互相衔接的两段半径不等的半圆弧，中间是一块薄金属片，粒子穿过时有动能损失。试判断粒子在上、下两段半圆径迹中哪段所需时间较长？（粒子重力不计）
如图10-16所示，带负电的粒子垂直磁场方向进入圆形匀强磁场区域，出磁场时速度偏离原方向60°角，已知带电粒子质量m=3×10-20kg，电量q=10-13C，速度v0=105m/s，磁场区域的半径R=3×10-1m，不计重力，求磁场的磁感应强度。
摆长为ι的单摆在匀强磁场中摆动，摆动平面与磁场方向垂直，如图10-14所示。摆动中摆线始终绷紧，若摆球带正电，电量为q，质量为m，磁感应强度为B，当球从最高处摆到最低处时，摆线上的拉力T多大？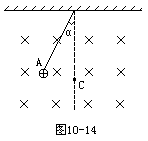
如图10-11所示，用绝缘丝线悬挂着的环形导体，位于与其所在平面垂直且向右的匀强磁场中，若环形导体通有如图所示方向的电流I，试判断环形导体的运动情况。
有一自由的矩形导体线圈，通以电流I′。将其移入通以恒定电流I的长直导线的右侧。其ab与cd边跟长直导体AB在同一平面内且互相平行，如图10-9所示。试判断将该线圈从静止开始释放后的受力和运动情况。（不计重力）
如图28-1所示，X轴上方有匀强磁场B，下方有匀强电场E。电量为q、质量为m、重力不计的粒子y轴上。X轴上有一点N(L.0)，要使粒子在y轴上由静止释放而能到达N点，问：(1)粒子应带何种电荷? (2)释放点M应满足什么条件? (3)粒子从M点运动到N点经历多长的时间?
平行金属，板长1.4米，两板相距30厘米，两板间
匀强磁场的B为1.3×10-3特斯拉，两板间所加电压
随时间变化关系如29-1图所示。当t=0时，有一个a
粒子从左侧两板中央以V=4×103米/秒的速度垂直于磁
场方向射入，如29-2图所示。不计a粒子的重力，求：
该粒子能否穿过金属板间区域?若不能，打在何处?若能， 则需多长时间? (已知a粒子电量q=3.2×10-19库，质量m=6.64×10-27千克)
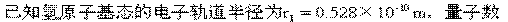
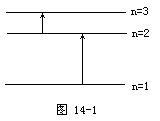
(1)求电子在基态轨道上运动时的动能。
(2)有一群氢原子处于量子数n=3的激发态。画一能级图，在图14－1上用箭头标明这些氢原子能发出哪几条光谱线。
(3)计算这几条光谱线中波长最短的一条的波长。(其中静电力恒量K=9.0×109N·m2/C2，电子电量e=1.6×10-19C，普朗克恒量h=6.63×10-34J·s，真空中光速c=3.0×108m/s)。
如图11－12所示，长为6m的导体AB在磁感强度B=0.IT的匀强磁场中，以AB上
的一点O为轴，沿着顺时针方向旋转。角速度ω=5rad／s，O点距A端为2m，求AB的电势差。
如图 11－20所示光滑平行金属轨道abcd，轨道的水平部分bcd处于竖直向上的匀强磁场中，bc部分平行导轨宽度是cd部分的2倍，轨道足够长。将质量相同的金属棒P和Q分别置于轨道的ab段和cd段。P棒位于距水平轨道高为h的地方，放开P棒，使其自由下滑，求P棒和Q棒的最终速度。
在图11－1中，CDEF为闭合线圈，AB为电阻丝。当滑动变阻器的滑动头向下滑动时，线圈CDEF中的感应电流在G处产生的磁感强度的方向是“·”时，电源的哪一端是正极？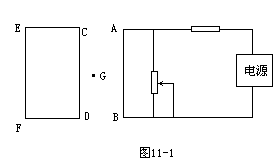
电阻为Ｒ的矩形导线框ａｂｃｄ，边长ａｂ＝ｌ、ａｄ＝ｈ、质量为ｍ，自某一高度自由落下，通过一匀强磁场，磁场方向垂直纸面向里，磁场区域的宽度为ｈ，如图35-1所示．若线框恰好以恒定速度通过磁场，线框内产生的焦耳热是多少．（不考虑空气阻力）
粤公网安备 44130202000953号