高中物理综合题

如图14所示，两根平行的光滑金属导轨与水平面成q角放置，导轨电阻忽略不计．在水平虚线L₁、L₂间有一导轨所在平面垂直的匀强磁场B，导体棒a、b的质量分别为m_a、m_b，电阻均为r，电动机通过绕过滑轮的细绳牵引着a由静止开始从导轨底部运动，b静止在导轨底部并与导轨接触良好。已知额定功率为P，重力加速度g，不计a、b之间电流的相互作用，如果电动机提供恒定的拉力，求：
（1）b棒刚开始运动，a棒的速度；
（2）b棒刚开始运动时a、b棒间的距离；
（3）如果b棒刚开始运动时电动机达到额定功率，该过程中，a棒产生的焦耳热是多少？

 

如图，一长为 L＝4m，质量为 M="0.5kg" 的木板 AB，正以 v ="14m/s" 的速度（相对地）在光滑水平地面上向右运动，此时，在木板 AB 的上表面 B 端处，一小物块m=2kg受水平向左的拉力 F="6N" 作用，从初速为零（相对地）开始运动．已知，m和M间的动摩擦因数μ=0.1，g 取10m/．试求：当小物块m从木板的B端运动到 A 端的过程，木板在地面上通过的位移大小？

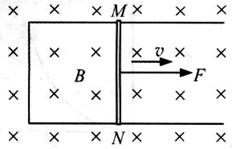
导体切割磁感线的运动可以从宏观和微观两个角度来认识。如图所示，固定于水平面的U形导线框处于竖直向下的匀强磁场中，金属直导线在与其垂直的水平恒力的作用下，在导线框上以速度做匀速运动，速度与恒力方向相同，导线始终与导线框形成闭合电路，已知导线电阻为，其长度，恰好等于平行轨道间距，磁场的磁感应强度为，忽略摩擦阻力和导线框的电阻。

（1）通过公式推导验证：在时间内，也等于导线中产生的焦耳热。
（2）若导线的质量=8.0，长度=0.1，感应电流=1.0，假设一个原子贡献1个自由电子，计算导线中电子沿导线长度方向定向移动的平均速率（下表中列出了一些你可能用到的数据）。

（3）经典物理学认为，金属的电阻源于定向运动自由电子和金属离子（金属原子失去电子后剩余部分）的碰撞，展开你想象的翅膀，给出一个合理的自由电子运动模型：在此基础上，求出导线中金属离子对一个自由电子沿导线长度方向的平均作用力的表达式。

如图5-8所示，滑块A、B的质量分别为m₁与m₂，m₁＜m₂，由轻质弹簧相连接置于水平的气垫导轨上，用一轻绳把两滑块拉至最近，使弹簧处于最大压缩状态后绑紧。两滑块一起以恒定的速率v₀向右滑动。突然轻绳断开，当弹簧伸至本身的自然长度时，滑块A的速度正好为0。求：
(1)绳断开到第一次恢复自然长度的过程中弹簧释放的弹性势能E_p；
(2)在以后的运动过程中，滑块B是否会有速度为0的时刻?试通过定量分析证明你的结论.

如图所示，空间内存在水平向右的匀强电场，在虚线MN的右侧有垂直纸面向里、磁感应强度为B的匀强磁场，一质量为m、带电荷量为+q的小颗粒自A点由静止开始运动，刚好沿直线运动至光滑绝缘的水平面C点，与水平面碰撞的瞬间小颗粒的竖直分速度立即减为零，而水平分速度不变，小颗粒运动至D处刚好离开水平面，然后沿图示曲线DP轨迹运动，AC与水平面夹角α = 30°，重力加速度为g，求：
（1）匀强电场的场强E；
（2）AD之间的水平距离d；
（3）已知小颗粒在轨迹DP上某处的最大速度为v_m，该处轨迹的曲率半径是距水平面高度的k倍，则该处的高度为多大？

产生的加速度为2m/s². 设运料车受到的阻力不变. 求：
(1) 运料车受到的阻力大小；
(2) 工人撤去水平推力时，车的加速度。

如图甲所示，物块A、B的质量分别是m_A=" 4.0kg" 和m_B= 3.0kg，用轻弹簧栓接相连放在光滑的水平地面上，物块B右侧与竖直墙相接触．另有一物块C从t =0时以一定速度向右运动，在t =" 4" s 时与物块A相碰，并立即与A粘在一起不再分开．物块C的v-t 图象如图乙所示．求：
（1）物块C的质量m_C；
（2）墙壁对物块B的弹力在4 s 到12 s 的时间内对B做的功W及对B的冲量I的大小和方向；
（3）B离开墙后的过程中弹簧具有的最大弹性势能E_P．

如图所示，一水平方向的传送带以恒定的速度v ="2" m/s沿顺时针方向匀速转动，传送带右端固定着一光滑的四分之一圆弧面轨道，并与弧面下端相切，圆弧轨道的半径R =" 0.45" m.一物体自圆弧面轨道最高点由静止滑下，物体与传送带之间的动摩擦因数为μ = 0.2，不计物体滑过曲面与传送带交接处时的能量损失，传送带足够长，g =10m/s². 求：

（1）物体滑上传送带向左运动的最远距离；
（2）物体第一次从滑上传送带到离开传送带所经历的时间；
（3）经过足够长的时间之后物体能否停下来？若能，请说明物体停下的位置. 若不能，请简述物体的运动规律。

[物理--选修3-4]

（1）在双缝干涉实验中，用绿色激光照射在双缝上，在缝后的屏幕上显示出干涉图样。若要增大干涉图样中两相邻亮条纹的间距，可选用的方法是________（最多选3个）。

A．	改用红色激光
B．	改用蓝色激光
C．	减小双缝间距
D．	将屏幕向远离双缝的位置移动
E．	将光源向远离双缝的位置移动

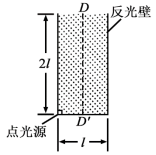
（2）一直桶状容器的高为 $2l$ ，底面是边长为 l的正方形；容器内装满某种透明液体，过容器中心轴 $DD\prime$ 、垂直于左右两侧面的剖面图如图所示。容器右侧内壁涂有反光材料，其他内壁涂有吸光材料。在剖面的左下角处有一点光源，已知由液体上表面的 D点射出的两束光线相互垂直，求该液体的折射率。

（1）水槽中，与水面接触的两根相同细杆固定在同一个振动片上。振动片做简谐振动时，两根细杆周期性触动水面形成两个波源。两波源发出的波在水面上相遇。在重叠区域发生干涉并形成了干涉图样。关于两列波重叠区域内水面上振动的质点，下列说法正确的是________。（填正确答案标号，最多选3个）            

A．	不同质点的振幅都相同
B．	不同质点振动的频率都相同
C．	不同质点振动的相位都相同
D．	不同质点振动的周期都与振动片的周期相同
E．	同一质点处，两列波的相位差不随时间变化

（2）如图，直角三角形ABC为一棱镜的横截面， $\angle \mathrm{A}=90°$ ， $\angle \mathrm{B}=30°$ 。一束光线平行于底边BC射到AB边上并进入棱镜，然后垂直于AC边射出。

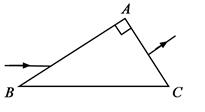
（i）求棱镜的折射率；

（ii）保持AB边上的入射点不变，逐渐减小入射角，直到BC边上恰好有光线射出。求此时AB边上入射角的正弦。

[物理--选修3-4]

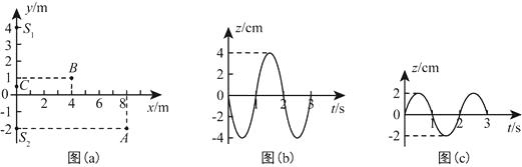
（1）如图（a），在 $\mathit{xy}$平面内有两个沿z方向做简谐振动的点波源 $S_1（0，4）$和 $S_2（0\mathit{，﹣}2）$．两波源的振动图线分别如图（b）和图（c）所示．两列波的波速均为1.00m/s．两列波从波源传播到点 $A（8\mathit{，﹣}2）$的路程差为________m，两列波引起的点 $B（4，1）$处质点的振动相互________（填“加强”或“减弱”），点 $C（0，0.5）$处质点的振动相互________（填“加强”或“减弱”）．

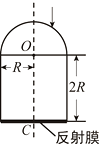
（2）如图，一玻璃工件的上半部是半径为R的半球体，O点为球心；下半部是半径为R、高为2R的圆柱体，圆柱体底面镀有反射膜．有一平行于中心轴OC的光线从半球面射入，该光线与OC之间的距离为0.6R．已知最后从半球面射出的光线恰好与入射光线平行（不考虑多次反射）．求该玻璃的折射率．

（1）如图，一个三棱镜的截面为等腰直角，为直角。此截面所在平面内的光线沿平行于边的方向射到边，进入棱镜后直接射到边上，并刚好能发生全反射。该棱镜材料的折射率为。(填入正确选项前的字母)

A．		B．
C．		D．

（2）波源和振动方向相同，频率均为，分别置于均匀介质中轴上的两点处，，如图所示。两波源产生的简谐横波沿轴相向传播，波速为。己知两波源振动的初始相位相同。求：

（）简谐横波的波长：

（）间合振动振幅最小的点的位置。

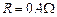如图所示，光滑且足够长的平行金属导轨和固定在同一水平面上，两导轨间距，电阻，导轨上静止放置一质量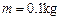、电阻的金属杆，导轨电阻忽略不计，整个装置处在磁感应强度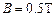的匀强磁场中，磁场的方向竖直向下，现用一外力沿水平方向拉杆，使之由静止起做匀加速运动并开始计时，若5s末理想电压表的读数为0.2V.求：
（1）5s末时电阻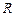上消耗的电功率；
（2）金属杆在5s末的运动速率；
（3）5s末时外力的功率.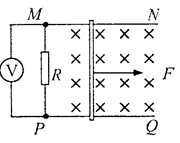
  

如图所示，在质量为M＝0.99kg的小车上，固定着一个质量为m＝10g、电阻R＝1W的矩形单匝线圈MNPQ，其中MN边水平，NP边竖直，高度l＝0.05m。小车载着线圈在光滑水平面上一起以v₀＝10m/s的速度做匀速运动，随后进入一水平有界匀强磁场（磁场宽度大于小车长度），完全穿出磁场时小车速度v₁＝2m/s。磁场方向与线圈平面垂直并指向纸内、磁感应强度大小B＝1.0T。已知线圈与小车之间绝缘，小车长度与线圈MN边长度相同。求：
（1）小车刚进入磁场时线圈中感应电流I的大小和方向；
（2）小车通过磁场的过程中线圈电阻的发热量Q；
（3）小车进入磁场过程中线圈克服安培力所做的功W。

、图（1）表示用水平恒力F拉动水平面上的物体，使其做匀加速运动。当改变拉力的大小时，相对应的匀加速运动的加速度a也会变化，a和F的关系如图（2）所示。

（1）该物体的质量为多少？
（2）在该物体上放一个与该物体质量相同的砝码，保持砝码与该物体相对静止，其他条件不变，请在图2的坐标上画出相应的a——F图线。
（3）由图线还可以得到什么物理量？（要求写出相应的表达式或数值）