高中物理计算题

在如图所示的倾角为θ的光滑斜面上，存在着两个磁感应强度大小为B的匀强磁场，区域I的磁场方向垂直斜面向上，区域Ⅱ的磁场方向垂直斜面向下，磁场的宽度均为L，一个质量为m、电阻为R、边长也为L的正方形导线框，由静止开始沿斜面下滑，当ab边刚越过GH进入磁场Ⅰ区时，恰好以速度 v₁做匀速直线运动；当ab边下滑到JP与MN的中间位置时，线框又恰好以速度v₂做匀速直线运动，从ab进入GH到MN与JP的中间位置的过程中，线框的动能变化量大小为△E_k，重力对线框做功的绝对值为W₁，安培力对线框做功的绝对值为W₂，下列说法中正确的有（     ）

A．v2=4v1

B．v2=v1

C．从ab进入GH到MN与JP的中间位置的过程中，机械能减小了W2

D．从ab进入GH到MN与JP的中间位置的过程中，线框动能的变化量大小为△Ek= W2－W1。

如图，xoy平面内存在着沿y轴正方向的匀强电场，一个质量为m、带电荷量为+q的粒子从坐标原点O以速度v₀沿x轴正方向开始运动。当它经过图中虚线上的M（，a）点时，撤去电场，粒子继续运动一段时间后进入一个矩形匀强磁场区域（图中未画出），又从虚线上的某一位置N处沿y轴负方向运动并再次经过M点。已知磁场方向垂直xoy平面（纸面）向里，磁感应强度大小为B，不计粒子的重力。试求：

⑴电场强度的大小；
⑵N点的坐标；
⑶矩形磁场的最小面积。

如图所示，半径R=0.40m的光滑半圆环轨道处于竖直平面内，半圆环与粗糙的水平地面相切于圆环的端点A。质量m=0.l0kg的小球与水平地面之间的动摩擦因数为μ=0.3，小球以初速度v₀="7.0" m/s在水平地面上向左运动4.0m后，冲上竖直半圆环，最后小球落在C点，取重力加速度g="10" m/s²，求：

（1）小球进入圆轨道通过A点时对轨道的压力；
（2）小球经过B点时速度；
（3）A、C间的距离；

在图所示的电路中，小量程电流表的内阻Rg=100Ω，满偏电流Ig=1mA，R₁=900Ω，R₂=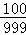Ω．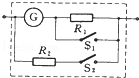

（1）当S₁和S₂均断开时，改装所成的表是什么表？量程为多大？
（2）当S₁和S₂均闭合时，改装所成的表是什么表？量程为多大？

如图所示，一个折射率为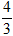的三棱镜的截面为等腰直角△ABC，∠A为直角。此截面所在平面内的一束光线沿与AB边成θ角（θ＜90°）的方向入射到AB边的中点P处，若要光线进入三棱镜后能射到AC边上且能在AC面上发生全反射，则cosθ应满足什么条件？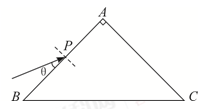

使用回旋加速器的实验需要把离子束从加速器中引出，离子束引出的方法有磁屏蔽通道法和静电偏转法等。质量为 $m$ ，速度为 $v$ 的离子在回旋加速器内旋转，旋转轨道时半径为 $r$ 的圆，圆心在 $O$ 点，轨道在垂直纸面向外的匀强磁场中，磁感应强度为 $B$ 。为引出离子束，使用磁屏蔽通道法设计引出器。引出器原理如图所示，一堆圆弧形金属板组成弧形引出通道，通道的圆心位于 $O`$ 点（ $O`$ 点图中未画出）。引出离子时，令引出通道内磁场的磁感应强度降低，从而使离子从P点进入通道，沿通道中心线从 $Q$ 点射出。已知 $OQ$ 长度为 $L$ 。 $OQ$ 与 $OP$ 的夹角为 $\theta$ ，

（1）求离子的电荷量 $q$ 并判断其正负；

（2）离子从 $P$ 点进入， $Q$ 点射出，通道内匀强磁场的磁感应强度应降为 $B`$ ，求 $B`$ ；

（3）换用静电偏转法引出离子束，维持通道内的原有磁感应强度 $B$ 不变，在内外金属板间加直流电压，两板间产生径向电场，忽略边缘效应。为使离子仍从 $P$ 点进入， $Q$ 点射出，求通道内引出轨迹处电场强度 $E$ 的方向和大小。

如图，一端开口、另一端封闭的细长薄壁玻璃管水平放置，内有用水银柱封闭的体积为10mL的某种理想气体．外界大气压为1标准大气压，环境温度为27℃，阿伏伽德罗常数约为6×10²³mol^－1，标准状况下1mol该气体体积约为22.4L．求：

①当环境温度降为0℃时(设大气压强不变)气体的体积；
②估算管中气体分子数目．(结果保留两位有效数字)

题左图为一理想变压器，ab为原线圈，ce为副线圈，d为副线圈引出的一个接头。原线圈输入正弦式交变电压的u-t图象如题右图所示。若只在ce间接一只R_ce="400" Ω的电阻，或只在de间接一只R_de="225" Ω的电阻,两种情况下电阻消耗的功率均为80W。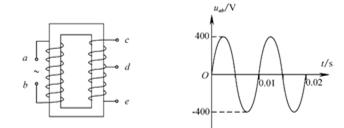

(1)请写出原线圈输入电压瞬时值u_ab的表达式；
(2)求只在ce间接400Ω的电阻时，原线圈中的电流I₁；
(3)求ce和de 间线圈的匝数比。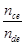

小明同学设计了一个"电磁天平"，如图1所示，等臂天平的左臂为挂盘，右臂挂有矩形线圈，两臂平衡。线圈的水平边长，竖直边长，匝数为。线圈的下边处于匀强磁场内，磁感应强度，方向垂直线圈平面向里。线圈中通有可在范围内调节的电流。挂盘放上待测物体后，调节线圈中电流使得天平平衡，测出电流即可测得物体的质量。（重力加速度取）

（1）为使电磁天平的量程达到，线圈的匝数至少为多少。

（2）进一步探究电磁感应现象，另选匝、形状相同的线圈，总电阻，不接外电流，两臂平衡，如图2所示，保持不变，在线圈上部另加垂直纸面向外的匀强磁场，且磁感应强度随时间均匀变大，磁场区域宽度。当挂盘中放质量为的物体时，天平平衡，求此时磁感应强度的变化率。

如图所示，匀强磁场的磁感应强度B=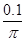T，矩形线圈的匝数N=100，边长L_ab=0.20m，L_bc=0.10m，以300r/min的转速匀速转动，从线圈平面通过中性面时开始计时，试求：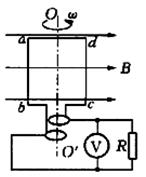

（1）交变电动势的瞬时值表达式；
（2）若线圈总电阻为2Ω，线圈外接电阻为8Ω，求出电流的瞬时值和电压表读数；
（3）求外接电阻在一个周期内产生的热量
（4）线圈由图示位置转过π/2的过程中，交变电动势的平均值及一个周期内流过外接电阻的电量。

一定质量的理想气体经历如图所示的A→B、B→C、C→A三个变化过程，设气体在状态A、B时的温度分别为T_A和T_B，已知T_A="300" K，求：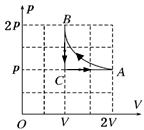

（1）T_B和T_c
（2）若气体从C→A的过程中做功为100J，同时吸热250J，则此过程中气体内能怎么改变？变化了多少？

倾角30°的斜面体放在水平地面上，小车与斜面之间光滑，斜面体与地面之间粗糙，用两根轻绳跨过两个固定的定滑轮一端接在小车上（滑轮与斜面没有连接），另一端分别悬挂质量为2m和m的物体A.B，当小车静止时两绳分别平行，垂直于斜面，如图所示，不计滑轮摩擦

（1）求小车的质量
（2）现使A.B位置互换，当系统再次静止时，地面与斜面体直接的摩擦力大小
（3）当A.B位置互换后，换用多大质量的小车可以使小车放在斜面上而斜面体与地面刚好没有摩擦力

如图所示，用一块长 $L_1=1.0m$ 的木板在墙和桌面间架设斜面，桌面高 $H=0.8m$ ，长 $L=1.5m$ 。斜面与水平桌面的倾角 $\theta$ 可在 $0~60°$ 间调节后固定。将质量 $m=0.2kg$ 的小物块从斜面顶端静止释放，物块与斜面间的动摩擦因数 $u_1=0.05$ ，物块与桌面间的动摩擦因数 $u_2$ ，忽略物块在斜面与桌面交接处的能量损失。（重力加速度取 $g=10m/s^2$ ；最大静摩擦力等于滑动摩擦力）

（1）求 $\theta$ 角增大到多少时，物块能从斜面开始下滑；（用正切值表示）

（2）当 $\theta$ 增大到 ${37}^{°}$ 时，物块恰能停在桌面边缘，求物块与桌面间的动摩擦因数 $u_2$ ；（已知 $\sin {37}^{°}=0.6$ ， $\cos {37}^{°}=0.8$ ）

（3）继续增大 $\theta$ 角，发现 $\theta =53°$ 时物块落地点与墙面的距离最大，求此最大距离 $x_m$ 。

已知金刚石的密度为ρ, 有一小块金刚石, 体积是V, 摩尔质量为M，阿伏加德罗常数为N_A,
求：（1）这小块金刚石中含有多少个碳原子?
（2）设想金刚石中碳原子是紧密地堆在一起的, 计算碳原子的直径。

质量为m的飞机模型，在水平跑道上由静止匀加速起飞，假定起飞过程中受到的平均阻力恒为飞机所受重力的k倍，发动机牵引力恒为F，离开地面起飞时的速度为v，重力加速度为g。求：

（1）飞机模型的起飞距离（离开地面前的运动距离）
（2）若飞机起飞利用电磁弹射技术，将大大缩短起飞距离。图甲为电磁弹射装置的原理简化示意图，与飞机连接的金属块（图中未画出）可以沿两根相互靠近且平行的导轨无摩擦滑动。使用前先给电容为C的大容量电容器充电，弹射飞机时，电容器释放储存电能所产生的强大电流从一根导轨流入，经过金属块，再从另一根导轨流出；导轨中的强大电流形成的磁场使金属块受磁场力而加速，从而推动飞机起飞。
①在图乙中画出电源向电容器充电过程中电容器两极板间电压u与极板上所带电荷量q的图象，在此基础上求电容器充电电压为U₀时储存的电能；
②当电容器充电电压为U_m时弹射上述飞机模型，在电磁弹射装置与飞机发动机同时工作的情况下，可使起飞距离缩短为x。若金属块推动飞机所做的功与电容器释放电能的比值为η，飞机发动的牵引力F及受到的平均阻力不变。求完成此次弹射后电容器剩余的电能。