
为3mg的拉力时就会断裂.现让环与球一起以 的
的
速度向右运动,在A处环被挡住而立即停止,A离右墙的水
平距离也为L.不计空气阻力,已知当地的重力加速度为 .
.
试求:
(1)在环被挡住而立即停止时绳对小球的拉力大小;
(2)在以后的运动过程中,球的第一次碰撞点离墙角B点的距离是多少?
(1)求车轮与冰雪路面间的动摩擦因数 ;
;
(2)若该车以 的速度在同样冰雪路面的平直公路上行驶,突然发现正前方停着一辆故障车,司机马上采取刹车措施,避免了相撞事故。问司机发现故障车时两车相距至少多远? (已知司机发现故障车至实施刹车的反应时间为
的速度在同样冰雪路面的平直公路上行驶,突然发现正前方停着一辆故障车,司机马上采取刹车措施,避免了相撞事故。问司机发现故障车时两车相距至少多远? (已知司机发现故障车至实施刹车的反应时间为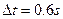 )
)
(3)在泥巴山上有一段同样冰雪路面的水平圆弧形弯道,圆弧半径 ,为保证该车不发生侧滑,汽车行驶的最大速度V为多少.
,为保证该车不发生侧滑,汽车行驶的最大速度V为多少.
如图所示,在匀速转动的圆盘上,沿半径方向放置以细线相连的质量均为m的A、B两个小物块,A离轴心 =20cm,B离轴心
=20cm,B离轴心 =30cm,A、B与盘面间相互作用的最大静摩擦力为其重力的0.4倍.求:
=30cm,A、B与盘面间相互作用的最大静摩擦力为其重力的0.4倍.求:
(1)当细线上出现张力时,圆盘转动的角速度 =?
=?
(2)欲使A、B与盘面间不发生相对滑动,则盘转动的最大角速度多大?(g=10m/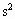 )
)
一级方程式汽车大赛中,一辆赛车总质量为m,一个路段的水平转弯半径为R,赛车转此弯时的速度为v,赛车形状都设计得使其上下方空气有一压力差——气动压力,从而增大了对地面的正压力.正压力与摩擦力的比值叫侧向附着系数,以η表示.要上述赛车转弯时不侧滑,则需要多大的气动压力?
如图所示,在光滑的圆锥顶端,用长为L=2m的细绳悬一质量为m=1kg的小球,圆锥顶角为2θ=74°。求:(1)当小球ω=1rad/s的角速度随圆锥体做匀速圆周运动时,细绳上的拉力。(2)当小球以ω=5rad/s的角速度随圆锥体做匀速圆周运动时,细绳上的拉力。
如图所示,在圆柱形屋顶中心天花板O点,挂一根L="3" m的细绳,绳的下端挂一个质量 为
为 的小球,已知绳能承受的最大拉力为10 N。小球在水平面内做圆周运动,当速度逐渐增大到绳断裂后,小球以
的小球,已知绳能承受的最大拉力为10 N。小球在水平面内做圆周运动,当速度逐渐增大到绳断裂后,小球以 的速度落在墙边。求这个圆柱形房屋的高度
的速度落在墙边。求这个圆柱形房屋的高度 和半径
和半径 。(g取10 m/s2)
。(g取10 m/s2)
游乐场的过山车的运动过程可以抽象为图所示模型。弧形轨道下端与圆轨道相接,使小球从弧形轨道上端A点静止滑下,进入圆轨道后沿圆轨道运动,最后离开。试分析A点离地面的高度h至少要多大,小球才可以顺利通过圆轨道最高点(已知圆轨道的半径为R,不考虑摩擦等阻力)。