如图所示,将一根光滑的细金属棒折成V形,顶角为2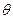 ,其对称轴竖直,在其中一边套上一个质量为m的小金属环P,
,其对称轴竖直,在其中一边套上一个质量为m的小金属环P,
(1)若固定V形细金属棒,小金属环P从距离顶点O为x的A点处由静止自由滑下,则小金属环由静止下滑至顶点O点时需多少时间?
(2)若小金属环P随V形细金属棒绕其对称轴以每秒n转匀速转动时,则小金属环离对称轴的距离为多少?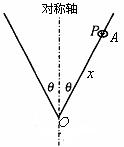
A、B两球质量分别为 和
和 ,用一劲度系数为
,用一劲度系数为 的弹簧相连,一长为
的弹簧相连,一长为 的细线与
的细线与 相连,置于水平光滑桌面上,细线的另一端拴在数值轴
相连,置于水平光滑桌面上,细线的另一端拴在数值轴 上,如图所示。当
上,如图所示。当 与
与 均以角速度
均以角速度 绕
绕 做匀速圆周运动且稳定后,弹簧长度为
做匀速圆周运动且稳定后,弹簧长度为 。求:
。求:
(1)此时绳子的张力大小。
(2)将线突然烧断的瞬间,A球的加速度是多大?
(1)要使盒子在最高点时盒子与小球之间恰好无作用力,则该盒子做匀速圆周运动的周期为多少?
(2)若盒子以第(1)问中周期的 做匀速圆周运动,则当盒子运动到图示球心与O点位于同一水平面位置时,小球对盒子的哪些面有作用力,作用力为多大?
做匀速圆周运动,则当盒子运动到图示球心与O点位于同一水平面位置时,小球对盒子的哪些面有作用力,作用力为多大?
如图所示,用一根长为l=1m的细线,一端系一质量为m=1kg的小球(可视为质点),另一端固定在一光滑锥体顶端,锥面与竖直方向的夹角θ=37°,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时,细线的张力为T。求(取g=10m/s2,结果可用根式表示):
(1)若要小球离开锥面,则小球的角速度ω0至少为多大?
(2)若细线与竖直方向的夹角为60°,则小球的角速度ω'为多大?
(3)细线的张力T与小球匀速转动的加速度ω有关,请在坐标纸上画出ω的取值范围在0到ω'之间时的T—ω2的图象(要求标明关键点的坐标值)。

“神舟六号”载人飞船在发射初期,宇航员的血液处于超重状态,严重时会产生黑视,甚至危及生命。
(1)假设载人飞船起飞时视为匀加速直线运动,加速度大小为60m/s2,方向竖直向上,两名宇航员在飞船内是躺在水平躺椅上的,则他们对躺椅的压力约为其重力的多少倍?(g=10m/s2)
(2)为了宇航员适应上述情况,必须进行专门的训练。训练的装置是半径为20m的水平坐舱,在电力的驱动下坐舱在水平面内做匀速圆周运动,若让坐舱在运动中的加速度大小为80m/s2,则坐舱每分钟应转动多少圈?(π约取3)