高中物理力学实验试题

下列说法正确的是（     ）

A．物体通过的路程不同，但位移可能相同

B．战斗机在战斗前扔掉副油箱，目的是减小惯性

C．物体速度的变化量越大，加速度越大

D．在国际单位制中力的单位用“牛顿”表示，“牛顿”是基本单位

从效果看，物体的各部分受到的重力作用可以认为都集中于一点，这一点叫做物体的重心，以下关于物体重心的说法中正确的是（     ）

A．物体的重心不一定在物体上

B．重心的位置与物体的质量分布无关

C．任何形状的物体，其重心都与它的几何中心重合

D．形状规则、质量分布均匀的物体，其重心在几何中心

关于重力，下列说法中正确的是（  ）

A．物体受到的重力大小和方向与物体的运动状态无关

B．抛出的石块轨迹是曲线，说明石块所受的重力方向在改变

C．自由下落的石块速度越来越大，说明石块所受重力越来越大

D．物体所受的重力作用于重心处，物体的其他部分不受重力作用

下列物理量中属于标量的是 （      ）

A．加速度

B．速度

C．速度变化量

D．时间

下面列举的几种速度中，指瞬时速度的是 （     ）

A．博尔特伦敦奥运会百米赛跑的速度是10.4 m/s

B．足球以12 m/s的速度射入球门

C．汽车车头经过路标时的速度是90 km/h

D．子弹在枪管里的速度是400 m/s

输出功率保持10kW的起重机起吊质量为500kg的静止重物，当重物升高到2m时，速度已经达到最大，若g取10m/s²，则
（1）最大速度为多少？
（2）此过程所用时间为多少?

节水喷灌系统已经在我国很多地区使用。某节水喷灌系统如图21所示，喷口距离地面的高度h = 1.8m，可将水沿水平方向喷出，并能沿水平方向旋转。喷水的最大速率v₀ = 15m/s，每秒喷出水的质量m₀ = 4.0kg/s。所用的水是从井下抽取的，井中水面离地面的高度H=1.95m，并一直保持不变。水泵由电动机带动，电动机电枢线圈电阻r=5.0Ω。电动机正常工作时，电动机的输入电压U = 220V，输入电流I=4.0A。不计电动机的摩擦损耗，电动机的输出功率等于水泵所需要的最大输入功率。水泵的输出功率与输入功率之比为水泵的抽水效率。计算时g取10m/s²，π取3。
（1）求这个喷灌系统所能喷灌的面积S；
（2）假设系统总是以最大喷水速度工作，求水泵的抽水效率η；
（3）假设系统总是以最大喷水速度工作，在某地区需要用蓄电池将太阳能电池产生的电能存储起来供该系统使用，根据以下数据求所需太阳能电池板的最小面积S_m。
太阳光传播到达地面的过程中大约有30%的能量损耗，
太阳辐射的总功率P₀ = 4×10²⁶W，
太阳到地球的距离R = 1.5×10¹¹m，
太阳能电池的能量转化效率约为15%，
蓄电池释放电能的效率约为90%。
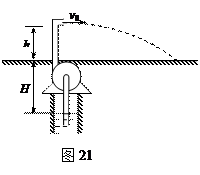
（已知球体的表面积）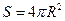

下列说法正确的是

A．在研究自行车后轮的转动情况时可以将自行车看作质点

B．电台报时说：“现在是北京时间8点整”，这里的“时间”实际上指的是时刻

C．质量和速度都是物体惯性大小的量度

D．做直线运动的物体当加速度方向与速度方向相同时，若加速度减小，速度反而增大

下列说法中正确的是

A．研究奥运会冠军刘翔的跨栏技术时可将刘翔看作质点

B．在某次铅球比赛中，某运动员以18.62米的成绩获得金牌，这里记录的成绩是比赛中铅球经过的路程

C．瞬时速度可理解为时间趋于零时的平均速度

D．“北京时间10点整”指的是时间，一节课40min指的是时刻

竖直细杆上套有一个1 kg的小圆环，圆环左侧系住一劲度系数k＝500 N/m的轻弹簧，已知弹簧与竖直方向的夹角为θ＝37°，圆环始终静止，则以下分析正确的是

A．当弹簧伸长量x＝2.5 cm时，圆环与竖直杆的摩擦力为零

B．当弹簧伸长量x＝0.5 cm时，圆环与竖直杆的弹力F＝1.5 N

C．保持弹簧伸长量不变，适度减小θ，圆环与细杆之间的弹力变小

D．保持弹簧伸长量不变，适度减小θ，圆环与细杆之间的摩擦力变小

质点做直线运动的位移x与时间t的关系为x=5t+t²（各物理量均采用国际单位制单位），则该质点（  ）

A．第1s内的位移是5m

B．前2s内的平均速度是7m/s

C．物体的加速度是5m/s^2

D．任意1s内的速度增加量都是2m/s

A、B、C三个物体从同一点出发，沿着一条直线运动的位移﹣时间（S﹣t）图象如图所示，下列说法中正确的是（ ）

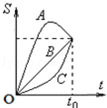
A．C物体做加速直线运动
B．A物体做曲线运动
C．三个物体在0～t₀时间内的平均速度v_A＞v_C＞v_B
D．三个物体在0～t₀时间内的平均速度v_A=v_B=v_C

下列说法正确的是（   ）

A．速度变化越大，则加速度越大

B．加速度，则物体一定做减速运动

C．加速度a越大，则物体的速度一定增大

D．若加速度方向与速度方向相同，加速度减小时，则速度反而增大

如图所示，是一种测定风力的仪器，P是质量为200g的金属球，固定在一根细长钢性的金属丝下端，当无风时金属球自然竖直下垂，有风时金属丝将偏离竖直方向，刻度盘上的角度就能反映出风力的大小。若某一时刻风从图示的水平方向吹向金属球P时，金属丝向左偏离竖直方向的角度θ=30°而处于静止状态。取g=10m/s²    则：

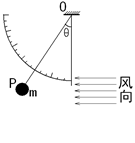
（1）此时风力和金属丝拉力分别有多大？
（2）有人说：“若角度变为2θ，则风力也变为原来的2倍”，你认为这个结论对不对？为什么？

一本书放在水平桌面上，下列说法正确的是(  )

A．桌面受到的压力实际就是书的重力

B．桌面受到的压力是由桌面形变形成的

C．桌面对书的支持力与书的重力是一对平衡力

D．同一物体在地球表面时赤道处重力略小，但形状规则物体的重心必在其几何中心