高中物理放射性同位素的应用综合题

(1)推力F的大小；
(2)若该人不改变力F的大小，只把力的方向变为与水平方向成30⁰角斜向上去拉这个静止的箱子，如图(b)所示，拉力作用2.0 s后撤去，箱子最多还能运动多长距离？(g取10 m/s²）．

(1)乙接棒前在接力区内跑过的距离。
(2)乙起跑时距甲的距离。

如图所示，弹簧的劲度系数为k，下端挂一个质量为m的物体，上端固定在天花板上，用托盘托住物体，使弹簧恰好没有形变。如果使托盘竖直向下做匀加速直线运动，加速度为a（a<g）。求经过多长时间物体和托盘相脱离。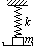

 

(1)卡车在减速与加速过程中的加速度．
(2)卡车在开始刹车后2 s末及10 s末的瞬时速度．
(3)卡车在这12 s内行驶的距离．

（1）滑板匀速直线运动的速度V₁；滑板与水面的夹角为q₁的大小。
（2）在运动过程中运动员可以通过调节滑板与水面的夹角来改变速度，当滑板与水面的夹角为q₂＝30°时，水平牵引力F₂=810N，运动员在竖直方向仍处平衡，滑板此时的速率V₂为多少？此时滑板的加速度a为多少？
（3）若运动员要做离开水面的空中特技动作，运动员可以先下蹬，使重心下降，使牵引力与水面的夹角a=15°斜向上。滑板与水面的夹角为q₃＝53°。速度为V₃="5m/s," 则在离水面前（水对滑板的作用力F_N还存在）牵引力F₃大小至少为多少？(sin15°=0.26)

（1）雪橇在开始阶段做什么运动？
（2）当雪橇的速度为5m／S时，它的加速度多大？
（3）空气的阻力系数k与雪橇与倾斜雪面间的动摩擦因数μ。（g＝10m／S²，Sin37⁰＝0．6）

⑴汽车在追上自行车前运动多长时间与自行车相距最远？此时他们之间的距离是多少？
⑵汽车至少要用多长时间才能追上自行车?
⑶试在右图的坐标中，作出此过程汽车和自行车的速度-时间图象．

（1）电梯在最初加速阶段的加速度a₁与最后减速阶段 
的加速度a₂的大小；
（2）电梯在3.0~13.0s时段内的速度v的大小；
（3）电梯在19.0s内上升的高度H。

（1）物体在第1秒内、第3秒内的位移分别为多少？
（2）第2秒内的位移为多少？
（3）经过多长时间，物体位移的大小为40.25m?

（1）2011年3月，日本地震引发海啸，继而福岛核电站（世界最大的核电站）发生核泄漏。关于核电站和核辐射，下列说法中正确的是        。
A.核反应堆发生的是轻核聚变反应
B.核反应堆发生的是重核裂变反应
C.放射性同位素的半衰期长短由核内部本身决定，与外部条件无关
D.放射性同位素的半衰期长短与地震、风力等外部环境有关
（2）如图所示，A、B两木块靠在一起放于光滑的水平面上，A、B的质量分别为m_A=2.0kg和m_B=1.5kg。一个质量为m_C=0.5kg的小铁块C以v₀=4m/s的速度滑到木块A上，离开木块A后最终与木块B一起匀速运动。木块A在铁块C滑离后的速度为v_A=0.4/m/s。求：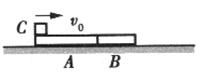

①铁块C在滑离A时的速度；
②最终木块B的速度。

一同学住在23层高楼的顶楼。他想研究一下电梯上升的运动过程。某天他乘电梯上楼时携带了一个质量为5kg的重物和一个量程足够大的台秤，他将重物放在台秤上，电梯从第l层开始启动，一直运动到第23层才停下。在这个过程中，他记录了台秤在不同时段内的读数如下表所示。

时间／s	台秤示数／N
电梯启动前	50.0
0～30	58.0
3.0～13.0	50.0
13.0～19.0	46.0
19.0以后	50.0

根据表格中的数据（g=l0m／s），求：
（1）电梯在最初加速阶段和最后减速阶段的加速度大小；
（2）电梯在中间阶段上升的速度大小；
（3）该楼房平均每层楼的高度．

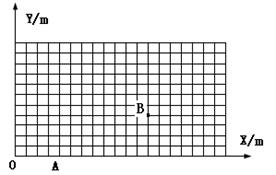
质量m=1kg的质点开始静止在xoy平面上原点O，某一时刻受到沿+x方向恒力F₁＝2N的作用。若力F₁作用一段时间t₁到达A点（图上位置未知）后撤去，立即施加沿y轴方向的力F₂，再经时间t₂=2s，质点恰好通过该平面上的B点，如图所示，B点的坐标为x = 12m，y =4m。在B点时撤去F₂并立即施加力F₃，经过t₃=2s质点到达C时速度刚好为零。不计其它作用。
（1）求力F₂大小；
（2）求力F₁的作用时间t₁；
（3）求力F₃的大小和方向；
（4）在图上标出C点的位置。（不必写出计算过程）

（1）物体向右运动的最远距离；
（2）在4s内物体运动的总路程。

一汽车做匀加速直线运动，在9s内通过相距72m的A、B两点，已知车通过B点的速度是通过A点速度的3倍。求汽车的加速度。