如图所示,用折射率 的玻璃做成内径为R,外径为
的玻璃做成内径为R,外径为 的半球形空心球壳,一束平行光射向此半球壳的外表面,与中心对称轴
的半球形空心球壳,一束平行光射向此半球壳的外表面,与中心对称轴 平行,试求:
平行,试求:
(1)球壳内部有光线射出的区域?(用与 所成夹角表示)
所成夹角表示)
(2)要使球壳内部没有光线射出,至少用多大面积的遮光板?
如图所示,平行玻璃板的厚度d=4cm,光线AB以入射角θ1=60°从空气射到平行玻璃板的上表面,经两次折射后从玻璃板的下表面射出。已知玻璃的折射率n= 。求出射光线CD相对于入射光线AB偏离的距离δ。
。求出射光线CD相对于入射光线AB偏离的距离δ。
半径为R的半球形介质截面如图所示,D为圆心,同一频率的单色光a、b相互平行,从不同位置进入介质,光线a在O点恰好产生全反射。光线b的入射角为45°,求:
①介质的折射率;
②光线a、b的射出点O与O′之间的距离。
如图所示,MN是一条通过透明球体球心的直线,在真空中波长为 的单色光束AB平行于MN射向球体,B为入射点,若出射光线CD与MN的交点P到球心O的距离是球半径的
的单色光束AB平行于MN射向球体,B为入射点,若出射光线CD与MN的交点P到球心O的距离是球半径的 倍,且与MN所成的夹角
倍,且与MN所成的夹角 ,求:
,求:
①透明球体的折射率 ;
;
②此单色光在透明球体中的波长 。
。
半径为R、介质折射率为n的透明圆柱体,过其轴线OO’的截面如图所示。位于截面所在平面内的一细束光线,以角i0由O点入射,折射光线由上边界的A点射出。当光线在O点的入射角减小至某一值时,折射光线在上边界的B点恰好发生全反射。求A、B两点间的距离。
如图所示,ABCD是封装手机LED闪光灯的圆柱形玻璃体的轴截面,玻璃体的厚度为d。厚度不计半径为r的圆形LED灯贴在玻璃体CD面上,圆心与CD面中心P重合,其发出的光从AB面射出,玻璃的折射率为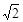 。不考虑光在AD和BC面上的反射,AB面上都有光线射出,求玻璃体的最大半径。
。不考虑光在AD和BC面上的反射,AB面上都有光线射出,求玻璃体的最大半径。
如图,为某种透明材料做成的三棱镜横截面,其形状是边长为a的等边三角形,现用一束宽度为a的单色平行光束,以垂直于BC面的方向正好入射到该三棱镜的AB及AC面上,结果所有从AB、AC面入射的光线进入后恰好全部直接到达BC面,试求: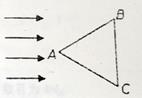
(1)该材料对此平行光束的折射率;
(2)这些到达BC面的光线从BC面折射出后,如果照射到一块平行于BC面的屏上形成光斑,则当屏到BC面的距离d满足什么条件时,此光斑分为两块?
如图,矩形ABCD为一水平放置的玻璃砖的截面,在截面所在平面内有一细束激光照射玻璃砖,入射点距底面的高度为h,反射光线和折射光线与底面所在平面的交点到AB的距离分别l1和l2,在截面所在平面内,改变激光束在AB面上入射点的高度与入射角的大小,当折射光线与底面的交点到AB的距离为l3时,光线恰好不能从底面射出,求此时入射点距离底面的高度H.
过去已知材料的折射率都为正值(n>0),现针对某些电磁波设计的人工材料,其折射率都为负值(n<0),称为负折射率材料,电磁波从空气射入这类材料时,折射定律和电磁波传播规律仍然不变,但是折射线与入射线位于法线的同一侧(此时折射角取负值)。现空气中有一上下表面平行厚度为d=30cm,折射率n=-1.732的负折射率材料,一束电磁波从其上表面以入射角i=60°射入,从下表面射出,
①请画出电磁波穿过该材料的示意图;
②求电磁波穿过该材料所用的时间。
半径为R的半圆柱形玻璃砖,横截面如图所示。O为圆心。已知玻璃的折射率为 。当光由玻璃射向空气时,发生全反射的临界角为45°,一束与MN平面成450的平行光束射到玻璃砖的半圆柱面上,经玻璃折射后,有部分光能从MN平面上射出。求能从MN平面射出的光束的宽度为多少?
。当光由玻璃射向空气时,发生全反射的临界角为45°,一束与MN平面成450的平行光束射到玻璃砖的半圆柱面上,经玻璃折射后,有部分光能从MN平面上射出。求能从MN平面射出的光束的宽度为多少?
如图所示,折射率为 、长为30m的细长透明体放在空气中,光从A端射入沿透明体传播到B端面。求光在透明体中从A端传播到B端所需时间的最小值和最大值。
、长为30m的细长透明体放在空气中,光从A端射入沿透明体传播到B端面。求光在透明体中从A端传播到B端所需时间的最小值和最大值。
雨过天晴,人们常看到天空中出现彩虹,它是阳光照射到空气中弥漫的水珠上时出现的现象,在说明这个现象时,需要分析光线射入水珠后的光路。一细束光线射入水珠,水珠可视为一个半径为R的球,球心O到入射光线的垂直距离为d,水的折射率为n。 在图上画出该束光线射入水珠内经一次反射后又从水珠中射出的光路图,并求这束光线从射向水珠到射出水珠一次偏转的角度(用反三角函数表示)。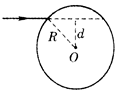
一棱镜的截面为直角三角形ABC,∠A=30o,斜边AB=a。棱镜材料的折射率为n= 。在此截面所在的平面内,一条光线以45o的入射角从AC边的中点M射入棱镜,求:光线从棱镜射出时,出射点的位置(不考虑光线沿原来路返回的情况)。
。在此截面所在的平面内,一条光线以45o的入射角从AC边的中点M射入棱镜,求:光线从棱镜射出时,出射点的位置(不考虑光线沿原来路返回的情况)。
如图所示,一个足够大的水池盛满清水,水深h="4" m,水池底部中心有一点光源A,其中一条光线斜射到水面上距A为l="5" m的B点时,它的反射光线与折射光线恰好垂直。
(i)求水的折射率n;
(ii)用折射率n和水深h表示水面上被光源照亮部分的面积(圆周率用π表示).