半径为R的半圆柱形玻璃砖,横截面如图所示。O为圆心。已知玻璃的折射率为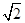 。当光由玻璃射向空气时,发生全反射的临界角为45°,一束与MN平面成450的平行光束射到玻璃砖的半圆柱面上,经玻璃折射后,有部分光能从MN平面上射出。求能从MN平面射出的光束的宽度为多少?
。当光由玻璃射向空气时,发生全反射的临界角为45°,一束与MN平面成450的平行光束射到玻璃砖的半圆柱面上,经玻璃折射后,有部分光能从MN平面上射出。求能从MN平面射出的光束的宽度为多少?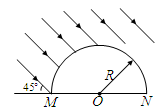
半径为R的半圆柱形玻璃砖,横截面如图所示。O为圆心。已知玻璃的折射率为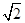 。当光由玻璃射向空气时,发生全反射的临界角为45°,一束与MN平面成450的平行光束射到玻璃砖的半圆柱面上,经玻璃折射后,有部分光能从MN平面上射出。求能从MN平面射出的光束的宽度为多少?
。当光由玻璃射向空气时,发生全反射的临界角为45°,一束与MN平面成450的平行光束射到玻璃砖的半圆柱面上,经玻璃折射后,有部分光能从MN平面上射出。求能从MN平面射出的光束的宽度为多少?