高中物理光的折射定律试题

如图所示为用某种透明材料制成的一块柱形棱镜的横截面图，圆弧CD是半径为R的四分之一圆周，圆心为O．光线从AB面上的M点入射，入射角i="60°" ，光进入棱镜后恰好在BC面上的O点发生全反射，然后由CD面射出．已知OB段的长度l=6cm，真空中的光速c=3.0×10⁸m/s．求：

①透明材料的折射率n
②光从M点传播到0点所用的时间t．

）如图所示为一等边三角形的某种透明介质ABC，边长为L，折射率为，底部中点O处有一点光源，试问能够从AB边射出光线的长度是多少？

如图所示，真空中有一下表面镀反射膜的平行玻璃砖，其折射率n＝，一束单色光与界面成θ=45⁰角斜射到玻璃砖表面上，最后在玻璃砖的右侧面竖直光屏上出现两个光点A和B，A和B相距h＝4.0cm。已知光在真空中的传播速度c=3.0xl0⁸m/s.

i.画出光路图；
ii.求玻璃砖的厚度

如图所示，某潜水员在检查装有透明液体的圆柱体容器，当潜水员的眼睛在容器中心轴位置且在液面下h₂=1m处时，他看到容器口处所有景物都出现在一个顶角为60°的倒立圆锥里，已知容器口距离容器液面的距离h₁=1m，圆柱体的横切面半径。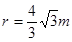

①求容器中液体的折射率。
②若一个身高h₃=1m的小孩站在离容器口边缘远的位置，小孩恰好能看到对面的容器底部，则容器中液体的深度为多少米？

半圆形玻璃砖的半径为R，光屏PQ置于直径的右端并与直径垂直，一复色光以30º的入射角射入玻璃砖的圆心。由于复色光中含有两种单色光，故在光屏上出现了两个光斑，玻璃对这两种色光的折射率分别为n₁= 和n₂=。

（1）求这两个光斑之间的距离。
（2）为使光屏上的光斑消失，复色光的入射角至少为多少?

如图所示，厚度为d的玻璃砖与水平实验桌面成45°角放置。红色激光束平行于水平桌面射到玻璃砖的表面，在桌面上得到两个光点A、B，已知玻璃砖对该红色激光的折射率为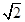。求：AB间的距离L。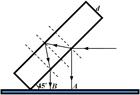

如图所示，OBCD为半圆柱体玻璃的横截面，OD为直径，一束由红光和紫光组成的复色光沿AO方向从真空斜射入玻璃，B、C点为两单色光的射出点(设光线在B、C处未发生全反射)．已知从B点射出的单色光由O到B的传播时间为t.

①若OB、OC两束单色光在真空中的波长分别为λ_B、λ_C，试比较λ_B、λ_C的大小(不必说明理由)；
②求从C点射出的单色光由O到C的传播时间t_C是多少？

在折射率为n，厚度为d的玻璃平板上方的空气中有一点光源S，从S发出的光线SA以入射角θ入射到玻璃板上表面，经过玻璃板后从下表面射出，如图所示。若沿此光线传播的光从光源 S 到玻璃板上表面的传播时间与在玻璃板中传播时间相等，点光源S到玻璃板上表面的垂直距离l应是多少？

如图所示，一束单色光从空气入射到棱镜的AB面上，经AB和AC两个面折射后从AC面进入空气。当出射角i’ 和入射角i相等时，出射光线相对于入射光线偏转的角度为θ。已知棱镜顶角为α，则计算棱镜对该色光的折射率表达式为（  ）

A．

B．

C．

D．

如图所示，MN为半圆形玻璃砖的对称轴．O为玻璃砖圆心，某同学在与MN平行的直线上插上两根大头针P₁、P₂，在MN上插大头针P₃，从P₃一侧透过玻璃砖观察P₁、P₂的像，调整P₃位置使P₃能同时挡住P₁、P₂的像，确定了的P₃位置如图所示，他测得玻璃砖直径D＝8 cm，P₁、P₂连线与MN之间的距离d₁＝2 cm，P₃到O的距离d₂＝6.92 cm。取＝1.73。求该玻璃砖的折射率。

两束平行的光斜射到平行玻璃砖，经玻璃砖折射后如图所示，则关于这两束光的说法中正确的是

A．A光的折射率比B光的折射率小

B．从玻璃砖下表面射出的两束光可能不平行

C．A光在水中的传播速度比B光在水中的传播速度小

D．增大A光在上界面的入射角，则进入玻璃砖的光线在下界面不可能发生全反射

如图所示，红色细光束a射到折射率为的透明球表面，入射角为45°，在球的内壁经过一次反射后，从球面射出的光线为b，则入射光线a与出射光线b之间的夹角α为

A．30°

B．45°

C．60°

D．75°

如图所示，一束截面为圆形（半径R）的平行白光垂直射向一玻璃半球的平面，经折射后在屏幕S上形成一个圆形彩色亮区。已知玻璃半球的半径为R，屏幕S至球心的距离为d（d>3R），不考虑光的干涉和衍射，试问：

①在屏幕S上形成的圆形亮区的最外侧是什么颜色?
②若玻璃半球对最外侧色光的折射率为，求出圆形亮区的最大半径。

如图所示为一透明玻璃半球，在其下面有一平行半球上表面水平放置的光屏。两束关于中心轴OO＇对称的激光束从半球上表面垂直射入玻璃半球，恰能从球面射出。当光屏距半球上表面h₁=40cm时，球面折射出的两束光线汇聚于光屏与OO＇轴的交点，当光屏距上表面h₂=70cm时，在光屏上形成半径r=40cm的圆形光斑。求该半球形玻璃的折射率。

如图所示，半径为R的半圆柱形玻璃柱，放置在直角坐标系xoy中，圆心与坐标系原点O重合，在第二象限中坐标为（-1.5R，R）的点A处，放置一个激光器（图中未画出），发出的两束细激光束a和b，其中，激光束a平行于x轴射向玻璃砖，激光束b沿AO方向射向玻璃砖。已知激光在玻璃中的折射率为，试作出激光束a和b通过玻璃砖的光路图，并证明a和b射出玻璃砖后是否相交。