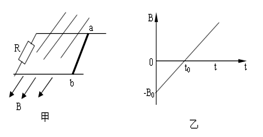
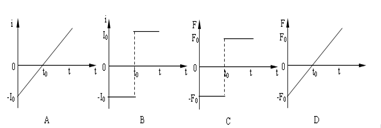
如图甲所示,光滑导轨水平放置在与水平方向夹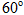 角斜向下的匀强磁场中,匀强磁场的磁感应强度B随时间t的变化规律如图乙所示(规定斜向下为正方向),导体棒ab垂直导轨放置,除电阻R的阻值外,其余电阻不计,导体棒ab在水平外力作用下始终处于静止状态。规定a→b的方向为电流的正方向,水平向右的方向为外力的正方向,则在0~t时间内,能正确反映流过导体棒ab的电流i和导体棒ab所受水平外力F随时间t变化的图象是 ( )
角斜向下的匀强磁场中,匀强磁场的磁感应强度B随时间t的变化规律如图乙所示(规定斜向下为正方向),导体棒ab垂直导轨放置,除电阻R的阻值外,其余电阻不计,导体棒ab在水平外力作用下始终处于静止状态。规定a→b的方向为电流的正方向,水平向右的方向为外力的正方向,则在0~t时间内,能正确反映流过导体棒ab的电流i和导体棒ab所受水平外力F随时间t变化的图象是 ( )
如图所示,水平导轨处于蹄形磁铁的磁场中,导体棒ab所在处的磁场方向竖直 (选填“向上”或“向下”);闭合电键,通电导体棒ab在磁场中受到的力称为 (选填“安培力”或“洛伦兹力”),由左手定则可知,该力的方向 (选填“向左”或“向右”)。

如图所示,光滑导轨与水平面成θ角,导轨宽L。匀强磁场磁感应强度为B。金属杆长也为L,质量为m,水平放在导轨上。当回路总电流为I1时,金属杆正好能静止。求:
(1)当B的方向垂直于导轨平面向上时B的大小;
(2)若保持B的大小不变而将B的方向改为竖直向上,应把回路总电流I2调到多大才能使金属杆保持静止?
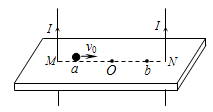
如图所示,两根长直导线竖直插入光滑绝缘水平桌面上的M、N两小孔中, O为M、N连线中点,连线上a、b两点关于O点对称。导线均通有大小相等、方向向上的电流。已知长直导线在周围产生的磁场的磁感应强度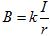 ,式中k是常数、I是导线中电流、r为点到导线的距离。一带正电的小球
,式中k是常数、I是导线中电流、r为点到导线的距离。一带正电的小球
以初速度v0从a点出发沿连线运动到b点。关于上述过程,下列说法正确的是( )
| A.小球先做加速运动后做减速运动 |
| B.小球一直做匀速直线运动 |
| C.小球对桌面的压力先减小后增大 |
| D.小球对桌面的压力一直在增大 |
如图所示,有一金属块放在垂直于表面C的匀强磁场中,磁感应强度B,金属块的厚度为d,高为h,当有稳恒电流I平行平面C的方向通过时,由于磁场力的作用,金属块中单位体积内参与导电的自由电子数目为(上下两面M、N上的电压为U)
A. |
B. |
C. |
D. |
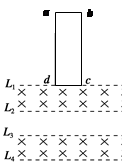
如图所示,在竖直方向上有四条间距均为L=0.5 m的水平虚线L1、L2、L3、L4,在L1L2之间、L3L4之间存在匀强磁场,大小均为1 T,方向垂直于纸面向里。现有一矩形线圈abcd,长度ad=3 L,宽度cd=L,质量为0.1 kg,电阻为1Ω,将其从图示位置静止释放(cd边与L1重合),cd边经过磁场边界线L3时恰好做匀速直线运动,整个运动过程中线圈平面始终处于竖直方向, cd边水平。(g="10" m/s2)则( )
| A.cd边经过磁场边界线L3时通过线圈的电荷量为0. 5 C |
| B.cd边经过磁场边界线L3时的速度大小为4 m/s |
| C.cd边经过磁场边界线L2和 L4的时间间隔为0.25s |
| D.线圈从开始运动到cd边经过磁场边界线L4过程,线圈产生的热量为0.7J |
如图所示,在一个范围足够大、垂直纸面向里的匀强磁场中,用绝缘细线将金属棒吊起,使其呈水平状态. 已知金属棒长L=0.1m,质量m=0.05kg,棒中通有I=10A的向右的电流,取g =10m/s2.
(1)若磁场的磁感应强度B=0.2T,求此时金属棒受到的安培力F的大小;
(2)若细线拉力恰好为零,求磁场的磁感应强度B的大小.
如图所示,有一区域足够大的匀强磁场,磁感应强度为B,磁场方向与水平放置的导轨垂直,导轨宽度为L,右端接有电阻R,MN是一根质量为m的金属棒,金属棒与导轨垂直放置,且接触良好,金属棒与导轨电阻均不计,金属棒与导轨间的动摩擦因数为μ,现给金属棒一水平冲量,使它以初速度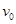 沿导轨向左运动,已知金属棒在整个运动过程中,通过任一截面的总电荷量为q,求:
沿导轨向左运动,已知金属棒在整个运动过程中,通过任一截面的总电荷量为q,求: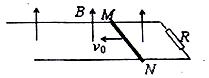
(1)金属棒运动的位移s;
(2)金属棒运动过程中回路产生的焦耳热Q;
(3)金属棒运动的时间t
如图所示,在倾角为θ=30°的斜面上,固定一宽L=0.25m的平行金属导轨,在导轨上端接入电源和变阻器.电源电动势E=12V,内阻r=1.0Ω一质量m=20g的金属棒ab与两导轨垂直并接触良好.整个装置处于磁感强度B=0.80T、垂直于斜面向上的匀强磁场中(导轨与金属棒的电阻不计).金属导轨是光滑的,取g=10m/s2,要保持金属棒在导轨上静止,求:
(1)金属棒所受到的安培力;
(2)通过金属棒的电流;
(3)滑动变阻器R接入电路中的阻值.
如图,用粗细均匀的电阻丝折成边长为L的平面等边三角形框架,每个边长L的电阻均为r,三角形框架的两个顶点与一电动势为E、内阻为r的电源相连接,垂直于框架平面有磁感应强度为B的匀强磁场,则三角形框架受到的安培力的合力大小为( )
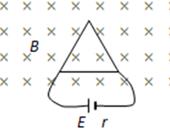
| A.0 | B. |
C.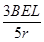 |
D. |
如图所示,宽度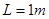 的足够长的U形金属框架水平放置,框架中连接电阻
的足够长的U形金属框架水平放置,框架中连接电阻 ,框架处在竖直向上的匀强磁场中,磁感应强度
,框架处在竖直向上的匀强磁场中,磁感应强度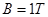 ,框架导轨上放一根质量为
,框架导轨上放一根质量为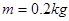 、电阻
、电阻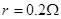 ,的金属棒
,的金属棒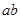 ,棒
,棒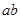 与导轨间的动摩擦因数
与导轨间的动摩擦因数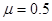 ,现用功率恒定
,现用功率恒定 的牵引力
的牵引力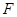 使棒从静止开始沿导轨运动(
使棒从静止开始沿导轨运动(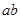 棒始终与导轨接触良好且垂直),当整个回路产生热量
棒始终与导轨接触良好且垂直),当整个回路产生热量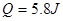 时刚好获得稳定速度,此过程中,通过棒的电量
时刚好获得稳定速度,此过程中,通过棒的电量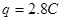 (框架电阻不计,
(框架电阻不计,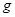 取
取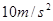 )求:
)求: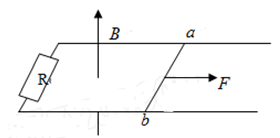
(1)当导体棒的速度达到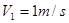 时,导体棒上
时,导体棒上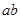 两点电势的高低?导体棒
两点电势的高低?导体棒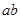 两端的电压?导体棒的加速度?
两端的电压?导体棒的加速度?
(2)导体棒稳定的速度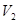 ?
?
(3)导体棒从静止到刚好获得稳定速度所用的时间?
如图所示,光滑导轨与水平面成θ角,导轨宽L.匀强磁场磁感应强度为B.金属杆长也为L,质量为m,水平放在导轨上.当回路总电流为I1时,金属杆正好能静止.求: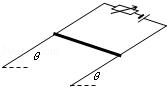
(1)B至少多大?这时B的方向如何?
(2)若保持B的大小不变而将B的方向改为竖直向上,应把回路总电流I2调到多大才能使金属杆保持静止?
如图所示,电阻不计、间距L=1m、足够长的光滑金属导轨ab、cd与水平面成θ=37°角,导轨平面矩形区域efhg内分布着磁感应强度的大小B=1T,方向垂直导轨平面向上的匀强磁场,边界ef、gh之间的距离D=1.4m。现将质量m=0.1kg、电阻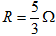 的导体棒P、Q相隔Δt=0.2s先后从导轨顶端由静止自由释放,P、Q在导轨上运动时始终与导轨垂直且接触良好,P进入磁场时恰好匀速运动,Q穿出磁场时速度为2.8m/s。已知重力加速度g=10m/s2,sin37°=0.6,求
的导体棒P、Q相隔Δt=0.2s先后从导轨顶端由静止自由释放,P、Q在导轨上运动时始终与导轨垂直且接触良好,P进入磁场时恰好匀速运动,Q穿出磁场时速度为2.8m/s。已知重力加速度g=10m/s2,sin37°=0.6,求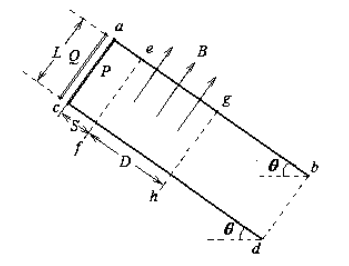
(1)导轨顶端与磁场上边界ef之间的距离S;
(2)从导体棒P释放到Q穿出磁场的过程,回路中产生的焦耳热Q总。
截流长直导线周围磁场的磁感应强度大小为 ,式中常量k>0,I为电流强度,r为距导线的距离。在水平长直导线MN正下方,矩形线圈abcd通以逆时针方向的恒定电流,被两根等长的轻质绝缘细线静止地悬挂,如图所示。开始时MN内不同电流,此时两细线内的张力均为
,式中常量k>0,I为电流强度,r为距导线的距离。在水平长直导线MN正下方,矩形线圈abcd通以逆时针方向的恒定电流,被两根等长的轻质绝缘细线静止地悬挂,如图所示。开始时MN内不同电流,此时两细线内的张力均为 。当MN通以强度为
。当MN通以强度为 的电流时,两细线内的张力均减小为
的电流时,两细线内的张力均减小为 ,当MN内的电流强度变为
,当MN内的电流强度变为 时,两细线的张力均大于
时,两细线的张力均大于

(1)分别指出强度为 的电流和方向;
的电流和方向;
(2)MN分别通以强度为 电流时,线框受到的安培力
电流时,线框受到的安培力 大小之比。
大小之比。