如图所示，光滑导轨与水平面成θ角，导轨宽L。匀强磁场磁感应强度为B。金属杆长也为L，质量为m，水平放在导轨上。当回路总电流为I1时，金属杆正好能静止。求：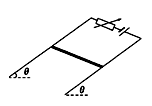
（1）当B的方向垂直于导轨平面向上时B的大小；
（2）若保持B的大小不变而将B的方向改为竖直向上，应把回路总电流I2调到多大才能使金属杆保持静止？
如图所示，两平行金属板A、B长度l=0.8m，间距d=0.6m．直流电源E能提供的电压足够大，位于极板左侧中央的粒子源可以沿水平方向向右连续发射比荷为
=l
×107C/kg、重力不计的带电粒子，射入板间的粒子速度均为v0=4×106m/s．在极板右侧有一个垂直纸面向里的匀强磁场，磁感应强度B=lT，分布在环带区域中，该环带的内外圆的圆心与两板间的中心重合于O点，环带的内圆半径Rl=
m．将变阻器滑动头由a向b慢慢滑动，改变两板间的电压时，带电粒子均能从不同位置穿出极板射向右侧磁场．
（1）问从板间右侧射出的粒子速度的最大值vm是多少?
（2）若粒子射出电场时，速度的反向延长线与v0所在直线交于O/点，试证明O/点与极板右端边缘的水平距离x=
，即O/与O重合，所有粒子都好像从两板的中心射出一样．
（3）为使粒子不从磁场右侧穿出，求环带磁场的最小宽度d．
如图所示，光滑的半球体固定在水平面上，其半径为R，有一小球（可视为质点）静止在半球体的最高点，小球受一扰动沿球面向下滚动，初速度忽略不计，重力加速度为g.
求：（1）小球落到地面时的速度大小；
（2）小球落到地面时速度的水平分量和竖直分量.
如图a所示，在真空中，半径为r的圆形区域内存在匀强磁场，磁场方向垂直纸面向外。在磁场右侧有一对平行正对金属板M和N，两板间距离为d，O1O2为两板的中心线。距平行金属板右端距离为l的位置放置竖直荧光屏其中心为O3，且O、O1、O2和O3在同一水平线上。有一粒子源发出电荷量为q、质量为m带正电的粒子束，以速率
从圆心O正下方的P点沿PO方向不断地射入磁场，粒子恰好由O1处沿O1O2进入金属板，粒子在板MN间的飞行时间均为T，现在将N板接地，如图（a）所示，U0是M板的电势大小如图（b）（c）所示，不计重力影响及粒子间的相互作用。
（1）求圆形区域磁场的磁感应强度B的大小；
（2）若M板上的电势如图（b）所示，t=0时M板电势为U0，求t=0时刻飞入电场的粒子最终打在荧光民间上距O3的距离；
（3）若M板上的电势如图（c）所示，粒子从O1点沿O1O2方向进入电场并射出，求它们射出电场时的速度大小及方向；
（4）若M板上的电势如图（c）所示，求荧光屏上能出现光亮区域的长度。
如图所示，在水平光滑轨道PQ上有一个轻弹簧其左端固定，现用一质量m=2.0kg的小物块（视为质点）将弹簧压缩后释放，物块离开弹簧后经过水平轨道右端恰好沿半圆轨道的切线进入竖直固定的轨道，小物块并进入半圆轨道后恰好能沿轨道运动，经过最低点后滑上质量M=8.0kg的长木板，最后恰好停在长木板最左端。已知竖直半圆轨道光滑且半径R=0.5m，物块与木板间的动摩擦因数μ=0.2，木板与水平地面间摩擦不计，取g=10m/s2
（1）弹簧具有的弹性势能；
（2）小物块滑到半圆轨道底端时对轨道的压力；
（3）木板的长度。
如图所示为某种弹射装置的示意图，轻弹簧左端与一固定挡板相连，光滑的水平导轨MN右端N处与水平传送带理想连接，传送带长L="4.0" m，皮带轮沿顺时针方向转动，带动皮带以速率v=3.0m/s匀速转动．两个质量均为m="1.0" kg的滑块A、B置于水平导轨上．第一次使滑块A压缩轻弹簧至某一位置，由静止释放，滑块A离开弹簧后以某一速度与B发生弹性碰撞，碰后滑块B以速度vB=2.0m/s滑上传送带，并从传送带右端P点滑出落至地面上的Q点，已知滑块B与传送带之间的动摩擦因数μ=0.20，重力加速度g取10m/s2．求：
（1）滑块B到达传送带右端P点时的速度；
（2）第二次实验时，使皮带轮沿逆时针方向转动，带动皮带以速率v="3.0" m/s匀速转动，仍要使滑块B落至Q点，则需将滑块A压缩弹簧至另一位置由静止释放，后与B发生弹性碰撞，求此过程弹簧对滑块A做的功W；
（3）在第二次实验过程中，滑块B在传送带上滑动过程中产生的热量Q．
粤公网安备 44130202000953号