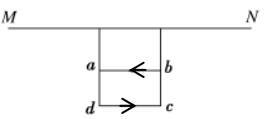
截流长直导线周围磁场的磁感应强度大小为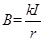 ,式中常量k>0,I为电流强度,r为距导线的距离。在水平长直导线MN正下方,矩形线圈abcd通以逆时针方向的恒定电流,被两根等长的轻质绝缘细线静止地悬挂,如图所示。开始时MN内不同电流,此时两细线内的张力均为
,式中常量k>0,I为电流强度,r为距导线的距离。在水平长直导线MN正下方,矩形线圈abcd通以逆时针方向的恒定电流,被两根等长的轻质绝缘细线静止地悬挂,如图所示。开始时MN内不同电流,此时两细线内的张力均为 。当MN通以强度为
。当MN通以强度为 的电流时,两细线内的张力均减小为
的电流时,两细线内的张力均减小为 ,当MN内的电流强度变为
,当MN内的电流强度变为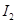 时,两细线的张力均大于
时,两细线的张力均大于
(1)分别指出强度为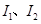 的电流和方向;
的电流和方向;
(2)MN分别通以强度为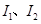 电流时,线框受到的安培力
电流时,线框受到的安培力 大小之比。
大小之比。
截流长直导线周围磁场的磁感应强度大小为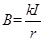 ,式中常量k>0,I为电流强度,r为距导线的距离。在水平长直导线MN正下方,矩形线圈abcd通以逆时针方向的恒定电流,被两根等长的轻质绝缘细线静止地悬挂,如图所示。开始时MN内不同电流,此时两细线内的张力均为
,式中常量k>0,I为电流强度,r为距导线的距离。在水平长直导线MN正下方,矩形线圈abcd通以逆时针方向的恒定电流,被两根等长的轻质绝缘细线静止地悬挂,如图所示。开始时MN内不同电流,此时两细线内的张力均为 。当MN通以强度为
。当MN通以强度为 的电流时,两细线内的张力均减小为
的电流时,两细线内的张力均减小为 ,当MN内的电流强度变为
,当MN内的电流强度变为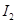 时,两细线的张力均大于
时,两细线的张力均大于

(1)分别指出强度为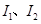 的电流和方向;
的电流和方向;
(2)MN分别通以强度为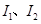 电流时,线框受到的安培力
电流时,线框受到的安培力 大小之比。
大小之比。