在竖直平面内建立直角坐标系xOy,其第一象限存在着正交的匀强电场和匀强磁场,电场强度的方向水平向右,磁感应强度的方向垂直纸面向里.一带电荷量为+q,质量为m的微粒从原点出发沿与x轴正方向的夹角为45°的初速度进入复合场中,正好做直线运动,当微粒运动到A(2L,2L)时,电场方向突然变为竖直向上(不计电场变化的时间),粒子继续运动一段时间后,正好垂直于y轴穿出复合场.(不计一切阻力)求:
(1)电场强度E大小;
(2)磁感应强度B的大小
如图所示,一个质量为m、电荷量为q,不计重力的带电粒子,从x轴上的P(a,0)点,以速度v沿与x轴正方向成60°角射入第一象限内的匀强磁场中,并恰好垂直于y轴射出第一象限.
求:匀强磁场的磁感应强度B的大小和粒子通过第一象限的时间.
如图所示,在空间建立O﹣xyz坐标系,水平向右为x轴正方向,竖直向上为y轴正方向,垂直纸面向外为z轴的正方向(图中未画出).一个放射源放在x轴上A点(﹣2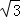 a,0),它能持续放出质量为m,带电量为+q,速度大小为v0的粒子,粒子射出方向与x轴夹角可调节,在第二象限区域外加场的作用下,粒子射出后总由y轴上C点(0,3a,0)以垂直于y轴的方向射入第一象限.而在y轴右侧相距为a处有与x轴垂直的足够大光屏PQ,y轴和光屏PQ间同时存在垂直纸面向外、大小为E0的匀强电场以及大小为B0=
a,0),它能持续放出质量为m,带电量为+q,速度大小为v0的粒子,粒子射出方向与x轴夹角可调节,在第二象限区域外加场的作用下,粒子射出后总由y轴上C点(0,3a,0)以垂直于y轴的方向射入第一象限.而在y轴右侧相距为a处有与x轴垂直的足够大光屏PQ,y轴和光屏PQ间同时存在垂直纸面向外、大小为E0的匀强电场以及大小为B0= 的匀强磁场,不计粒子的重力.
的匀强磁场,不计粒子的重力.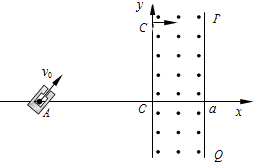
(1)若在第二象限整个区域仅存在沿﹣y轴方向的匀强电场,求该电场的场强E;
(2)若在第二象限整个区域仅存在垂直纸面的匀强磁场,求磁感应强度B;
(3)在上述两种情况下,粒子最终打在光屏上的位置坐标.
如图所示,在空间中存在垂直纸面向外,宽度为d的有界匀强磁场。一质量为m、带电荷量为q的粒子自下边界的P点处以速度v沿与下边界成30°角的方向垂直射入磁场,恰能垂直于上边界射出,不计粒子重力,题中d、m、q、v均为已知量。则
(1)粒子带何种电荷?
(2)磁场磁感应强度为多少?
一个质量为m带电量为q的小球,以初速度v0自离地面h高度处水平抛出.重力加速度为g,空气阻力忽略不计.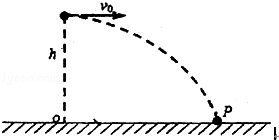
(1)求小球自抛出到第一次落地点P的过程中发生的水平位移x的大小.
(2)若在空间加一个竖直方向的匀强电场,发现小球以相同方式水平抛出后做匀速直线运动,请判断电场的方向并求出电场强度E的大小.
(3)若在空间再加一个垂直纸面的匀强磁场,发现小球以相同方式水平抛出后第一次落地点仍然是P.已知OP间的距离大于h,请判断磁场的方向并求出磁感应强度B的大小.
如图, OAC的三个顶点的坐标分别为O(0,0)、A(0,L)、C(
OAC的三个顶点的坐标分别为O(0,0)、A(0,L)、C( ,0),在
,0),在 OAC区域内有垂直于xOy平面向里的匀强磁场。在t=0时刻,同时从三角形的OA边各处以沿y轴正向的相同速度将质量均为m,电荷量均为q的带正电粒子射入磁场,已知在t=t0时刻从OC边射出磁场的粒子的速度方向垂直于y轴。不计粒子重力和空气阻力及粒子间相互作用。
OAC区域内有垂直于xOy平面向里的匀强磁场。在t=0时刻,同时从三角形的OA边各处以沿y轴正向的相同速度将质量均为m,电荷量均为q的带正电粒子射入磁场,已知在t=t0时刻从OC边射出磁场的粒子的速度方向垂直于y轴。不计粒子重力和空气阻力及粒子间相互作用。
(1)求磁场的磁感应强度B的大小;
(2)若从OA边两个不同位置射入磁场的粒子,先后从OC边上的同一点P(P点图中未标出)射出磁场,求这两个粒子在磁场中运动的时间t1与t2之间应满足的关系;
(3)从OC边上的同一点P射出磁场的这两个粒子经过P点的时间间隔与P点位置有关,若该时间间隔最大值为 ,求粒子进入磁场时的速度大小。
,求粒子进入磁场时的速度大小。
把一根长为L=10cm的直导线垂直磁感线方向放入如图所示的匀强磁场中.试问:
(1)当导线中通以I1=2A的电流时,导线受到的安培力大小为1.0×10﹣7N,该磁场的磁感应强度B的大小为多少?
(2)若该导线中通以I2=3A的电流,试求此时导线所受安培力F的大小,并在图中画出安培力的方向.
磁感应强度为矢量,它可以分解为几个分量。
(1)如果北半球某处地磁场的磁感应强度大小为B,与水平方向的夹角为θ且斜向下,那么该处地磁场的磁感应强度的水平分量和竖直分量各为多大?
(2)如果地理南、北极和地磁北、南极是重合的,那么在赤道上空磁场的竖直分量是多大?在极地上空地磁场的水平分量是多大?
如图(a)所示,平行金属板A和B间的距离为d,现在A、B板上加上如图(b)所示的方波形电压,t=0时A板比B板的电势高,电压的正向值为U0,反向值也为U0,现有由质量为m的带正电且电荷量为q的粒子组成的粒子束,从AB的中点O以平行于金属板方向OO'的速度v0= 不断射入,所有粒子在AB间的飞行时间均为T,不计重力影响.试求:
不断射入,所有粒子在AB间的飞行时间均为T,不计重力影响.试求:
(1)粒子打出电场时位置离O'点的距离范围;
(2)若要使打出电场的粒子经某一垂直纸面的圆形区域匀强磁场偏转后,都能通过圆形磁场边界的一个点处,而便于再收集,则磁场区域的最小半径和相应的磁感强度是多大?
在赤道上,地磁场可以看成沿南北方向的均匀磁场.如果赤道某处的磁感应强度大小为0.5×10﹣4T,在赤道上有一根东西方向的直导线,长25米,通有从西向东的电流20A,问地磁场对这根直导线的作用力有多大?方向如何?
电磁炮是一种理想的兵器,它的主要原理如图所示,1982年,澳大利亚国立大学制成了能把2.2g的弹体(包括金属杆EF的质量)加速到10km/s的电磁炮(常规炮弹的速度约为2km/s),若轨道宽2m,长为100m,通以恒定电流10A。(不计轨道摩擦)求:
(1)弹体的加速度;
(2)轨道间所加匀强磁场的磁感应强度为多大?
(3)磁场力的最大功率为多大?
(1)下列过程中,没有利用电磁波的是_______________。
A.电视机接收卫星电视信号 B.移动电话通话
C.电风扇通电后正常运转 D.雷达发现飞机
(2)[3分]物理学中描述电场强弱的物理量是_________。
A.电流 B.电荷量 C.电场强度 D.磁感应强度
(3)[3分]在国际单位制中,电容的单位是____________
A.法拉 B.伏特 C.安培 D.欧姆
(4)[3分]下列说法正确的是__________
A.电磁感应现象是牛顿发现的
B.交流发电机发出的电流方向不变
C.升压变压器的原、副线圈匝数相同
D.远距离输电要用高电压,是为了减少输电线上的电能损失
(5)[4分]当螺线管中通入如图所示的电流时,位于它B端附近的小磁针____________(填“会”或“不会”)发生偏转,螺线管A端的磁极是____________(填“N极”或“S极”)
(6)[6分] 一根长L=0.2m的直导线,通有I=2A的电流,放入磁感应强度B=1T的匀强磁场中。问:
①当导线方向与磁场方向平行时,导线会不会受到安培力?
②当导线方向与磁场方向垂直时,导线受到的安培力是多大?
如图a所示,水平直线MN下方有竖直向上的匀强电场,现将一重力不计,比荷 的正电荷置于电场中的O点由静止释放,经过
的正电荷置于电场中的O点由静止释放,经过 后,电荷以
后,电荷以 的速度通过MN进入其上方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过NM时为t=0时刻),计算结果可用
的速度通过MN进入其上方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过NM时为t=0时刻),计算结果可用 表示。
表示。
(1)求O点与直线MN之间的电势差
(2)求图b中 时刻电荷与O点的水平距离
时刻电荷与O点的水平距离
(3)如果在O点右方 处有一垂直于MN的足够大的挡板,求电荷从O点出发运动到挡板所需的时间
处有一垂直于MN的足够大的挡板,求电荷从O点出发运动到挡板所需的时间
磁强计的原理如图所示,电路中有一段金属导体,它的横截面积的边长等于a的正方形,放在沿x正方向的匀强磁场中,导体中通有沿y方向、电流强度为I的电流,已知金属导体单位体积中的自由电子数为n,电子电量为e,金属导体导电过程中,自由电子所做的定向移动可以认为是匀速运动,测出导体上下两侧面间的电势差为U.求:
(1)导体上、下侧面哪个电势较高?
(2)磁场的磁感应强度是多大?