高中物理理想气体的状态方程计算题

如图所示，气缸放置在水平平台上，活塞质量为10kg，横截面积50cm²，厚度不计．当温度为27℃时，活塞封闭的气柱长10cm，若将气缸倒过来放置时，活塞下方的空气能通过平台上的缺口与大气相通．g取10m／s²，不计活塞与气缸之间的摩擦，大气压强保持不变

①将气缸倒过来放置，若温度上升到127℃，此时气柱的长度为20cm，求大气压强．
②分析说明上述过程气体是吸热还是放热．

如图所示，一个绝热的气缸竖直放置，内有一个绝热且光滑的活塞，中间有一个固定的导热性良好的隔板，隔板将气缸分成两部分，分别密封着两部分理想气体 A 和 B。活塞的质量为m，横截面积为S，与隔板相距h。现通过电热丝缓慢加热气体，当A气体吸收热量Q时，活塞上升了h，此时气体的温度为T₁。已知大气压强为P₀，重力加速度为g。

①加热过程中，若A气体内能增加了₁，求B气体内能增加量₂
②现停止对气体加热，同时在活塞上缓慢添加砂粒，当活塞恰好回到原来的位置时A气体的温度为T₂。求此时添加砂粒的总质量。

lmol理想气体的压强p与体积V关系如图所示。气体在状态A时的压强为p₀、体积为V₀，热力学温度为T₀，在状态B时的压强为2p₀，体积为2V₀，AB为直线段。已知该气体内能与温度成正比U=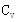T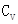（ 为比例系数）。求：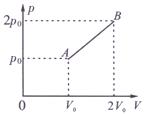

①气体在B状态时的热力学温度；
②气体从状态A变化到状态B的过程中，吸收的热量。

如图，柱形容器内用不漏气的轻质绝热活塞封闭一定量的理想气体，容器外包裹保温材料。开始时活塞至容器底部的高度为H₁，容器内气体温度与外界温度相等。在活塞上逐步加上多个砝码后，活塞下降到距容器底部H₂处，气体温度升高了△T；然后取走容器外的保温材料，活塞位置继续下降，最后静止于距容器底部H₃处：已知大气压强为p₀。求：气体最后的压强与温度。

）（某同学用吸管吹出一球形肥皂泡，开始时，气体在口腔中的温度为37℃，吹出后的肥皂泡体积为0.5L，温度为0℃，肥皂泡内、外压强差别不大，均近似等于1个标准大气压。试估算肥皂泡内的气体分子个数和这部分气体在口腔内的体积。

一定质量的理想气体从状态A变化到状态B再变化到状态C，其状态变化过程的p-V图象如图所示。已知该气体在状态A时的温度为27℃。求：
①该气体在状态B、C时的温度分别为多少摄氏度？
②该气体从状态A到状态C的过程中是吸热还是放热？传递的热量是多少？

某学校科技兴趣小组，利用废旧物品制作了一个简易气温计：在一个空葡萄酒中插入一根两端开口的玻璃管，玻璃管内有一段长度可忽略的水银柱，接口处用蜡密封，将酒瓶水平放置，如图所示．已知：该装置密封气体的体积为480cm³，玻璃管内部横截面积为0.4cm²，瓶口外的有效长度为48cm．当气温为7℃时，水银柱刚好处在瓶口位置．

①求该气温计能测量的最高气温．
②假设水银柱从瓶口处缓慢移动到最右端的过程中，密封气体从外界吸收3J热量，问：在这一过程中该气体的内能如何变化？变化了多少？（已知大气压为1×10⁵Pa）

某同学利用DIS实验系统研究一定质量理想气体的状态变化，实验后计算机屏幕显示如下的图象。已知在状态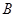时气体的体积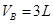，求：

①气体在状态的压强； ②气体在状态的体积。

）（如图所示，玻璃管的横截面S=1cm²，在玻璃管内有一段质量为m ="0.1" kg的水银柱和一定量的理想气体，当玻璃管平放时气体柱的长度为l₀="10" cm，现把玻璃管正立，过较长时间后再将玻璃管倒立，经过较长时间后，求玻璃管由正立至倒立状态，水银柱相对于管底移动的距离是多少？（假设环境温度保持不变，大气压强取P₀=1×10⁵Pd）

如图所示，内壁光滑的气缸竖直放置，在距气缸底部l=36cm处有一与气缸固定连接的卡环，活塞与气缸底部之间封闭了一定质量的气体。当气体的温度T₁=300K、大气压强时，活塞与气缸底部之间的距离，已知活塞面积为，不计活塞的质量和厚度，现对缸内气体加热，使活塞缓慢上升当温度上升至时，求：

①封闭气体此时的压强；
②该过程中气体对外做的功；

如图所示，竖直放置的U形管左端封闭，右端开口，左管横截面积为右管横截面积的2倍，在左管内用水银封闭一段长为l、温度为T₁的空气柱，左右两管水银面高度差为hcm，外界大气压为h₀ cm Hg。

①若向右管中缓慢注入水银，直至两管水银面相平（原右管中水银没全部进入水平部分），求在右管中注入水银柱的长度h₁(以cm为单位)；
②在两管水银面相平后，缓慢升高气体的温度至空气柱的长度为开始时的长度l，求此时空气柱的温度T＇。

有一空的薄金属筒，高h₁="10" cm。某同学将其开口向下，自水银表面处缓慢压入水银中，如图所示。设大气和水银温度恒定，筒内空气无泄漏，大气压强P。="75" cmHg，不计气体分子间的相互作用。当金属筒被压入水银表面下h₂="0.7" m处时，求金属筒内部空气柱的高度h。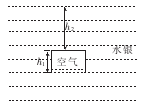

如图所示，圆柱形容器内用活塞封闭一定质量的理想气体，已知容器横截面积为S，活塞重为G，大气压强为p₀。若活塞固定，封闭气体温度升高1℃，需吸收的热量为Q₁；若活塞不固定，仍使封闭气体温度升高1℃，需吸收的热量为Q₂。不计一切摩擦，在活塞可自由移动时，封闭气体温度升高1℃，活塞上升的高度h应为多少？

如图所示，在一个圆柱玻璃瓶中插入一根两端开口的玻璃管，接口处用蜡密封，圆柱玻璃瓶内有一部分水银封住密闭气体，管横截面积为S₁＝1 cm²、瓶的横截面积S₂＝6 cm²，细管内水银长度为h＝4 cm，封闭气体长度为L＝6 cm。大气压强为p₀＝76 cmHg，气体初始温度为T₁＝300 K，上管足够长。

①缓慢升高气体温度，求水银刚好全部进入玻璃管内时的温度T₂；
②若把温度升到427℃时，水银的下表面到瓶底的距离。

一定质量的理想气体从状态A变化到状态B再变化到状态C，其状态变化过程的P-V图象如图所示。已知该气体在状态A时的温度为27℃。求：

①该气体在状态B、C时的温度各为多少℃；
②该气体从状态A到状态C的过程中是吸热还是放热？传递的热量是多少.