一次演习中,一空降特战兵实施空降,在飞机悬停180m高的空中后,空降特战兵从机舱中一跃而下,把空降特战兵空降假定为如下过程:空降特战兵出飞机舱后先做自由落体运动,下落了2s后打开辅伞,特战兵立即做匀速运动,过了一段时间后打开主伞,特战兵立即做匀减速直线运动,匀减速运动6s后到达了“敌方”的地面,此时空降特战兵的速度恰好为零,g取10m/s2.求:
(1)空降特战兵做自由落体运动下落的距离是多少?
(2)空降特战兵从出机舱到着地总共花了多少时间?
质量为0.1kg的小球从空中某高度由静止开始下落到地面,该下落过程对应的v-t图像如图所示,小球与水平地面每次碰撞后离开地面时的速度大小为碰撞前的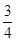 ,小球运动受到空气阻力大小恒定,取
,小球运动受到空气阻力大小恒定,取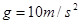 ,下列说法正确的是( )
,下列说法正确的是( )

| A.小球受到空气阻力大小0.3N |
B.小球上升时的加速度大小为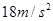 |
| C.小球第一次上升的高度为0.375m |
| D.小球第二次下落的时间为 |
在2009年10月第十一届全运会上,一个质量为60kg的运动员,从离水平网面3.2m高处自由下落,着网后沿竖直方向蹦回到离水平网面5.0m高处.已知运动员与网接触的时间为1.2s.若把在这段时间内运动员对网的作用力当作恒力处理,求此力的大小.(g取10m/s2)
如图所示,一网球运动员将球在边界处正上方水平向右击出,球刚好过网落在图中位置(不计空气阻力),相关数据如图,下列说法中正确的是
| A.击球点高度h1与球网高度h2之间的关系为h1 =1.8h2 |
B.若保持击球高度不变,球的初速度 只要不大于 只要不大于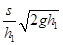 ,一定落在对方界内 ,一定落在对方界内 |
C.任意降低击球高度(仍大于 ),只要击球初速度合适,球一定能落在对方界内 ),只要击球初速度合适,球一定能落在对方界内 |
| D.任意增加击球高度,只要击球初速度合适,球一定能落在对方界内 |
一质点从离地面125 m高处由静止开始下落,不计空气阻力,g取10 m/s2,求:
(1)第1s质点下落的高度;
(2)质点从开始下落到落地所用的时间;
(3)落地前1s质点下落的高度。
一个自由下落的物体,在最后1s内下落的距离为45m。求自由下落的总高度h与总时间t。(g=10m/s2)
如图,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的环,环套在竖直固定的光滑直杆上,光滑定滑轮与直杆的距离为d.现将环从与定滑轮等高的A处由静止释放,当环沿直杆下滑距离也为d时(图中B处),下列说法正确的是(重力加速度为g)( )
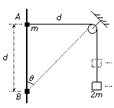
| A.小环刚释放时轻绳中的张力一定大于2mg |
| B.小环到达B处时,重物上升的高度也为d |
C.小环在B处的速度与重物上升的速度大小之比等于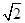 |
D.小环在B处时的速度为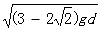 |
某个质量为m的物体在从静止开始下落的过程中,除了重力之外还受到水平方向的大小、方向都不变的力F= mg的作用。
mg的作用。
(1)这个物体在沿什么样的轨迹运动?求它在时刻t的速度大小。
(2)建立适当的坐标系,写出这个坐标系中代表物体运动轨迹的x、y之间的关系式。
某物体做自由落体运动( ),则
),则
| A.第2s的平均速度为15m/s |
| B.后一秒的位移总比前一秒的位移多5m |
| C.前一秒的平均速度总比后一秒的平均速度小10m/s |
| D.第7s的位移为65m |
如图所示,A、B两棒长均为l=1.0 m,A的下端和B的上端相距s=20 m。若A、B同时运动,A做自由落体运动,B做竖直上抛运动,初速度v0=40 m/s。(g取10 m/s2)求∶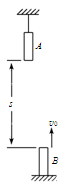
(1)A、B两棒何时相遇;
(2)从相遇开始到分离所需的时间。
在一次低空跳伞演练中,当直升飞机悬停在离地面224m高处时,伞兵离开飞机做自由落体运动.运动一段时间后,打开降落伞,展伞后伞兵以12.5m/s2的加速度匀减速下降.为了伞兵的安全,要求伞兵落地速度最大不得超过5m/s,(取g=10m/s2)求:
(1)伞兵展伞时,离地面的高度至少为多少?着地时相当于从多高处自由落下?
(2)伞兵在空中的最短时间为多少?
一个从静止做自由落体运动的小球,下落2s砸坏并穿过一水平放置在空中的玻璃板,因而小球失去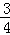 的速度,如果小球又用了2s到达地面,求玻璃板离地面的高度?(g取10m/s2)
的速度,如果小球又用了2s到达地面,求玻璃板离地面的高度?(g取10m/s2)
如图所示,质量为 的半圆轨道小车静止在光滑的水平地面上,其水平直径AB长度为
的半圆轨道小车静止在光滑的水平地面上,其水平直径AB长度为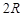 ,现将质量也为
,现将质量也为 的小球从距A点正上方
的小球从距A点正上方 高处由静止释放,然后由A点经过半圆轨道后从B冲出,在空中能上升的最大高度为
高处由静止释放,然后由A点经过半圆轨道后从B冲出,在空中能上升的最大高度为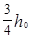 (不计空气阻力),则( )
(不计空气阻力),则( )
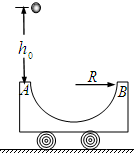
| A.小球和小车组成的系统动量守恒 |
B.小车向左运动的最大距离为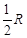 |
| C.小球离开小车后做斜上抛运动 |
D.小球第二次能上升的最大高度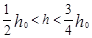 |
(12分)在一次低空跳伞训练中,当直升机悬停在离地面224 m高处时,伞兵离开飞机做自由落体运动.运动一段时间后,打开降落伞,展伞后伞兵以12.5 m/s2的加速度匀减速下降.为了伞兵的安全,要求伞兵落地速度最大不得超过5 m/s,求:(取g=10 m/s2)
(1)伞兵展伞时,离地面的高度至少为多少?着地时相当于从多高处自由落下?
(2)伞兵在空中的最短时间为多少?
如图所示,AB和CDO都是处于竖直平面内的光滑圆形轨道,OA处于水平位置.AB是半径为R=2m的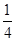 圆周轨道,CDO是半径为r=1m的半圆轨道,最高点O处固定一个竖直弹性挡板.D为CDO轨道的中点.已知BC段是水平粗糙轨道,与圆弧形轨道平滑连接.已知BC段水平轨道长L=2m,与小球之间的动摩擦因数μ=0.4.现让一个质量为m=1kg的小球P从A点的正上方距水平线OA高H自由下落.(g=10m/s2)
圆周轨道,CDO是半径为r=1m的半圆轨道,最高点O处固定一个竖直弹性挡板.D为CDO轨道的中点.已知BC段是水平粗糙轨道,与圆弧形轨道平滑连接.已知BC段水平轨道长L=2m,与小球之间的动摩擦因数μ=0.4.现让一个质量为m=1kg的小球P从A点的正上方距水平线OA高H自由下落.(g=10m/s2)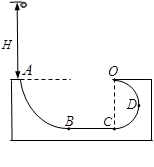
(1)当H=8.55m时,问此球第一次到达O点对轨道的压力;
(2)当H=8.55m时,试通过计算判断此球是否会脱离CDO轨道.如果会脱离轨道,求脱离位置距C点的竖直高度.如果不会脱离轨道,求静止前球在水平轨道经过的路程;
(3)H取值满足什么条件时,小球会脱离CDO轨道?