已知地球质量为M,万有引力常量为G ,现有一质量为m的卫星绕地球做匀速圆周运动,其轨道半径为r,问:
(1)卫星受到的万有引力多大?
(2)卫星所在高度处的重力加速度多大?
(2)卫星的运动周期为多大?
“嫦娥三号”是我国嫦娥工程第二阶段的登月探测器,于2013年12月2日凌晨l时30分在西昌卫星发射中心发射,携“玉兔号”月球车奔向距地球38万千米的月球;6日17时53分,“嫦娥三号”成功实施近月制动,顺利进入距月面平均高度约100千米的环月轨道;14日21时11分在月球正面的虹湾地区,“嫦娥三号”又成功实现月面软着陆,开始对月表形貌与地质构造等进行科学探测。若“嫦娥三号”环月飞行时运行周期为T,环月轨道(图中圆轨道Ⅰ)距月球表面高为h。已知月球半径为R,引力常量为G,求:
(1)月球的质量;
(2)月球表面的重力加速度。
图为"嫦娥三号"探测器在月球上着陆最后阶段的示意图.首先在发动机作用下,探测器受到推力在距月球高度为处悬停(速度为
,
远小于月球半径);接着推力改变,探测器开始竖直下降,到达距月面高度为
处的速度为
,此后发动机关闭,探测器仅受重力下落至月面.已知探测器总质量为
(不包括燃料),地球和月球的半径比为
,质量比为
,地球表面附近的重力加速度为
,求:

(1)月球表面附近的重力加速度大小及探测器刚接触月面时的速度大小;
(2)从开始竖直下降到刚接触月面时,探测器机械能的变化。
石墨烯是近些年发现的一种新材料,其超高强度及超强导电、导热等非凡的物理化学性质有望使21世纪的世界发生革命性的变化,其发现者由此获得2010年诺贝尔物理学奖。用石墨烯制作超级缆绳,人类搭建"太空电梯"的梦想有望在本世纪实现。科学家们设想,通过地球同步轨道站向地面垂下一条缆绳至赤道基站,电梯仓沿着这条缆绳运行,实现外太空和地球之间便捷的物资交换。

(1)若"太空电梯"将货物从赤道基站运到距地面高度为的同步轨道站,求轨道站内质量为
的货物相对地心运动的动能。设地球自转角速度为
,地球半径为
。
(2)当电梯仓停在距地面高度的站点时,求仓内质量
的人对水平地板的压力大小。取地面附近重力加速度
,地球自转角速度
,地球半径
。
已知地球的自转周期和半径分别为和
,地球同步卫星
的圆轨道半径为
。卫星B沿半径为
的圆轨道在地球赤道的正上方运行,其运行方向与地球自转方向相同。求:
(1)卫星做圆周运动的周期;
(2)卫星和
连续地不能直接通讯的最长时间间隔(信号传输时间可忽略)。
万有引力定律揭示了天体运动的规律与地上物体运动规律具有内在的一致性。
(1)用弹簧秤称量一个相对于地球静止的小物体的重量,随称量位置的变化可能会有不同的结果。已知地球的质量为,自转周期为
,引力常量为
。将地球看作是半径为
,质量均匀分布的球体,不考虑空气的影响。设在地球北极地面称量时,弹簧秤的读数
。
a.若在北极上空处称量,弹簧秤的读数为
,求比值
的表达式(并就
的情形算出具体数值,(计算结果保留两位有效数字)
b.若在赤道地面处称量,弹簧秤的读数为,求比值
的表达式
(2)设想地球绕太阳公转的半径为,太阳的半径为
,地球的半径为
,三者均减小为现在的1.0%,太阳和地球的密度均匀且不变,仅考虑太阳和地球之间的相互作用,以现实地球的1年为标准,计算"设想地球"的一年将变为多长?
“重力探矿”是常用的探测石油矿藏的方法之一。其原理可简述如下:如图,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油,假定区域周围岩石均匀分布,密度为 ;石油密度远小于
;石油密度远小于 ,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。
,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。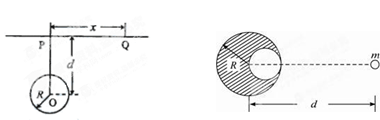
(1)“重力探矿”利用了“割补法”原理:如图所示,在一个半径为R、质量为M的均匀球体中,紧贴球的边缘挖去一个半径为R/2的球形空穴后,剩余的阴影部分对位于球心和空穴中心连线上、与球心相距d的质点m的引力是多大?
(2)设球形空腔体积为V,球心深度为d(远小于地球半径), =x,利用“割补法”原理:如果将近地表的球形空腔填满密度为
=x,利用“割补法”原理:如果将近地表的球形空腔填满密度为 的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力
的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力 来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值
来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值 (
( 在OP方向上的分量)
在OP方向上的分量)
(3)若在水平地面上半径L的范围内发现:重力加速度反常值在 与
与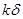 (k>1)(
(k>1)( 为常数)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。
为常数)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。
我国启动“嫦娥工程”以来,分别于2007年10月24日和2010年10月1日将“嫦娥一号”和“嫦娥二号”成功发射,“嫦娥三号”亦有望在2013年落月探测90天,并已给落月点起了一个富有诗意的名字——“广寒宫”.
(1)若已知地球半径为R,地球表面的重力加速度为g,月球绕地球运动的周期为T,月球绕地球的运动近似看做匀速圆周运动,求月球绕地球运动的轨道半径r;
(2)若宇航员随登月飞船登陆月球后,在月球表面某处以速度v0竖直向上抛出一个小球,经过时间t小球落回抛出点.已知月球半径为r月,引力常量为G,试求月球的质量M月.
在地球的圆轨道上运动的人造卫星,它到地球表面的距离等于地球半径R,设在地球表面的重力加速度为g,
求:(1)地球的第一宇宙速度
(2)卫星运动的周期
如图所示,“神舟”十号宇宙飞船控制中心的大屏幕上出现的一幅卫星运行轨迹图,它记录了飞船在地球表面垂直投影的位置变化;图中表示在一段时间内飞船绕地球圆周飞行四圈,依次飞经中国和太平洋地区的四次轨迹①、②、③、④,图中分别标出了各地点的经纬度(如:在轨迹①通过赤道时的经度为西经157.5°,绕行一圈后轨迹②再次经过赤道时经度为180°……),若地球质量为M,地球半径为R,万有引力恒量为G 。请完成以下问题:
①飞船轨道平面与赤道平面的夹角为 ;
②飞船绕地球运行的周期(写出分析原因及计算过程)
③飞船运行轨道距地球表面的高度(写出计算过程)。
两颗卫星在同一轨道平面内绕地球做绕向相同的匀速圆周运动,设地球平均半径为R,a卫星离地面高为R,b卫星离地面高为3R,若某时该两卫星正好同时通过地面同一点正上方,试求从两卫星位于地面同一点正上方开始,两卫星第一次出现最远距离的时间是a卫星周期的几倍?
已知太阳光从太阳射到地球需时间t,地球公转轨道可近似看成圆轨道,公转周期为T,地球半径为R,地球表面的重力加速度为g ,试计算太阳质量M与地球质量m之比。(真空中的光速为c)
“神舟”七号飞船的成功发射为我国在2010年实现探月计划﹣﹣“嫦娥工程”获得了宝贵的经验.假设月球半径为R,月球表面的重力加速度为g0 ,飞船在距月球表面高度为3R的圆形轨道Ⅰ运行,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入月球近月轨道Ⅲ绕月球做圆周运动,万有引力常量为G,求:
(1)飞船在轨道Ⅲ上的运行速率;
(2)飞船在轨道Ⅰ绕月球运行一周所需的时间.
(3)飞船在A点处点火后瞬间与点火前相比,速度是变大还是变小?
2013年12月14日晚,嫦娥三号探测器成功落月,这是中国首次实现地外天体软着陆,着陆器落月过程的最后时刻,有以上几个关键阶段:①着陆器距离月面100m时保持悬停,对着陆区进行检测,选择安全的着陆点;②随后发动机维持一定推力缓慢下降,降至距月面4m时关闭发动机,着陆器依靠自身重力在月面着陆.已知月球半径约为地球半径的 ,月球质量约为地球质量的
,月球质量约为地球质量的 ,着陆器质量约为1000kg,地球表面重力加速度g=10m/s2,根据以上数据计算:
,着陆器质量约为1000kg,地球表面重力加速度g=10m/s2,根据以上数据计算:
(1)着陆器距月面100m悬停时,发动机产生的推力为多大?
(2)若关闭发动机时速度为零,则最后依靠自身重力着陆,落至月面的速度为多大?
已知地球与火星的质量之比是8∶1,半径之比是 2∶1,在地球表面用一恒力沿水平方向拖一木箱,箱子能获得10m/s2的加速度。将此箱子送上火星表面,仍用该恒力沿水平方向拖木箱,则木箱产生的加速度为多大?已知木箱与地球和火星表面的动摩擦因数均为0.5,地球表面g = 10m/s2。