高中物理万有引力定律及其应用计算题

某人造地球卫星绕地球做匀速圆周运动，它离地面的高度为地球半径R的3倍，已知地面附近的重力加速度为g，引力常量为G．求：
（1）地球的质量；
（2）这颗人造地球卫星的向心加速度和周期．

2013年6月，我国成功实现目标飞行器“神舟十号”与轨道空间站“天宫一号”的对接．如图所示，已知“神舟十号”从捕获“天宫一号”到实现对接用时t，这段时间内组合体绕地球转过的角度为θ（此过程轨道不变，速度大小不变），地球半径为R，地球表面重力加速度为g，万有引力恒量G，不考虑地球自转；求：（1）地球质量M；（2）组合体运动的周期T；（3）组合体所在圆轨道离地高度H。

嫦娥三号将于今年12月发射，嫦娥三号及其月球车实现一系列重大突破，将完成在月球表面软着陆和巡视探测，实现中华民族五千年来九天揽月的梦想．一位勤于思考的同学为探月机械人设计了如下实验：在月球表面以初速度v₀竖直上抛出一个物体，测得物体的经过t时间落回．通过查阅资料知道月球的半径为R，引力常量为G，若物体只受月球引力的作用，上抛高度很小．求：
（1）月球的质量
（2）嫦娥三号在距月球表面高R处绕月球圆周运行的速率．

某星球半径为R =" 6×" 10⁶ m，假设该星球表面上有一倾角为θ = 30°的固定斜面，一质量为m =" 1" kg的小物块在力，作用下从静止开始沿斜面向上运动，力F始终与斜面平行，如图甲所示。已知小物块和斜面间的动摩擦因数，力F随位移x变化的规律如图乙所示（取沿斜面向上的方向为正向），如果小物块运动12 m时速度恰好为零，已知万有引力常量G =" 6.67" × 10^-11 N·m²/kg²。试求：（计算结果保留一位有效数字）

（1）该星球表面上的重力加速度g的大小；
（2）该星球的平均密度。

中子星是恒星演化过程的一种可能结果，它的密度很大。现有一中子星，观测到它的自转周期为T=s。问该中子星的最小密度应是多少才能维持该星的稳定，不致因自转而瓦解。计算时星体可视为均匀球体。（引力常数G=6．6710m/kg．s）

有些航空母舰上装有帮助飞机起飞的弹射系统，已知某型号的舰载飞机在跑道上加速时可能产生的最大加速度为5m/s²，当飞机的速度达到50m/s时才能离开航空母舰起飞，设航空母舰处于静止状态．问：
（1）若要求该飞机滑行160m后起飞，弹射系统必须使飞机具有多大的初速度？
（2）若航空母舰上不装弹射系统，设航空母舰甲板长为L=160m，为使飞机仍能此舰上正常起飞，这时可以先让航空母舰沿飞机起飞方向以某一速度匀速航行，则这个速度至少为多少？

经过用天文望远镜长期观测，人们在宇宙中已经发现了许多双星系统，通过对它们的研究，使我们对宇宙中物质的存在形式和分布情况有了较深刻的认识，双星系统由两个星体组成，其中每个星体的线度都远小于两星体之间的距离，一般双星系统距离其他星体很远，可以当做孤立系统来处理。现根据对某一双星系统的光度学测量确定，该双星系统中每个星体的质量都是M，两者相距L，它们正围绕两者连线的中点做圆周运动。试求：
（1）该双星系统的运动周期；
（2）若该实验中观测到的运动周期为T_观测，且。为了理解T_观测 与T_计算的不同，目前有一种流行的理论认为，在宇宙中可能存在一种望远镜观测不到的暗物质。作为一种简化模型，我们假定在以这两个星体连线为直径的球体内均匀分布这种暗物质。若不考虑其他暗物质的影响，根据这一模型和上述观测结果确定该星系间这种暗物质的密度。

两颗卫星在同一轨道平面绕地球做匀速圆周运动，地球半径为R，a卫星离地面的高度等于R，a卫星离地面高度为3R，则
（1）a、b两卫星周期之比T_a∶T_b是多少?
（2）若某时刻两卫星正好同时通过地面同一点的正上方，则a至少经过多少个周期两卫星相距最远?

如图所示为我国“嫦娥一号卫星”从发射到进入月球工作轨道的过程示意图。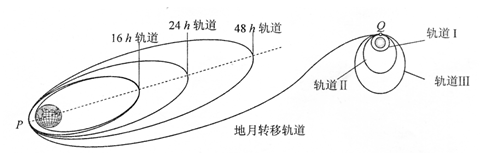

在发射过程中经过一系列的加速和变轨，卫星沿绕地球“48小时轨道”在抵达近地点P时，主发动机启动，“嫦娥一号卫星”的速度在很短时间内由v₁提高到v₂，进入“地月转移轨道”，开始了从地球向月球的飞越。“嫦娥一号卫星”在“地月转移轨道”上经过114小时飞行到达近月点Q时，需要及时制动，使其成为月球卫星。之后，又在绕月球轨道上的近月点Q经过两次制动，最终进入绕月球的圆形工作轨道I。已知“嫦娥一号卫星”质量为m₀，在绕月球的圆形工作轨道I上运动的周期为T，月球的半径r_月，月球的质量为m_月，万有引力恒量为G。
（1）求卫星从“48小时轨道”的近地点P进入“地月转移轨道”过程中主发动机对“嫦娥一号卫星”做的功（不计地球引力做功和卫星质量变化）；
（2）求“嫦娥一号卫星”在绕月球圆形工作轨道I运动时距月球表面的高度；
（3）理论表明：质量为m的物体由距月球无限远处无初速释放，它在月球引力的作用下运动至距月球中心为r处的过程中，月球引力对物体所做的功可表示为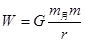。为使“嫦娥一号卫星”在近月点Q进行第一次制动后能成为月球的卫星，且与月球表面的距离不小于圆形工作轨道I的高度，最终进入圆形工作轨道，其第一次制动后的速度大小理论上应满足什么条件？

质量为m的卫星发射前静止在地球赤道表面。假设地球可视为质量均匀分布的球体，半径为R。
（1）已知地球质量为M，自转周期为T，引力常量为G。求此时卫星对地表的压力N的大小；
（2）卫星发射后先在近地轨道上运行（轨道离地面的高度可以忽略不计），运行的速度大小为v₁，之后经过变轨成为地球的同步卫星，此时离地面高度为H，运行的速度大小为v₂。
a．求比值；
b．若卫星发射前随地球一起自转的速度大小为v₀，通过分析比较v₀、 v₁、v₂三者的大小关系。

（由于地球自转的影响，地球表面的重力加速度会随纬度的变化而有所不同：若地球表面两极处的重力加速度大小为g₀，在赤道处的重力加速度大小为g，地球自转的周期为T，引力常量为G，地球可视为质量均匀分布的球体。求： (1)地球半径R；(2)地球的平均密度；
(3)若地球自转速度加快，当赤道上的物体恰好能“飘”起来时，求地球自转周期T'。

若“嫦娥”探月卫星为绕月球地卫星，利用该卫星可对月球进行成像探测。已知卫星距离月球表面高为h，绕行周期为T，月球绕地球公转的周期为T₀，月球绕地球公转的轨道半径为R₀，地球半径为R，月球半径为r，引力常量为G，光速为c，月球绕地球及卫星绕月球均做匀速圆周运动。求：

（1）地球的质量M和月球的质量m及月球的第一宇宙速度v；
（2）如图所示，当绕月球地轨道的平面与月球绕地球公转的轨道平面垂直（即与地心到月心的连线垂直）时，绕月球地卫星向地球地面发送照片需要的最短时间t。

一个质量为1500 kg行星探测器从某行星表面竖直升空，发射时发动机推力恒定，发射升空后8 s末，发动机突然间发生故障而关闭；如图所示为探测器从发射到落回出发点全过程的速度图象；已知该行星表面没有大气，不考虑探测器总质量的变化；求：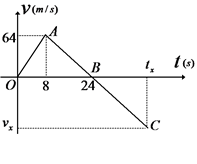

（1）探测器在行星表面上升达到的最大高度；
（2）探测器落回出发点时的速度；
（3）探测器发动机正常工作时的推力。

质量为100 kg行星探测器从某行星表面竖直发射升空，发射时发动机推力恒定，发射升空后8 s末，发动机突然间发生故障而关闭，探测器从发射到落回出发点全过程的速度图象如图所示。已知该行星半径是地球半径的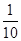，地球表面重力加速度为10m/s²，该行星表面没有大气，不考虑探测器总质量的变化。求：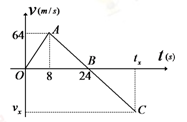

（1）探测器发动机推力大小；
（2）该行星的第一宇宙速度大小。

宇航员到达某星球后，他在该星球上取得一矿石，测得其质量为M₀ ，体积为V₀ ,重力为G₀ ，若矿石密度等于该星球平均密度 ，引力常量为G ，该星球视为球形，求该星球半径的表达式。