若“嫦娥”探月卫星为绕月球地卫星，利用该卫星可对月球进行成像探测。已知卫星距离月球表面高为h，绕行周期为T，月球绕地球公转的周期为T0，月球绕地球公转的轨道半径为R0，地球半径为R，月球半径为r，引力常量为G，光速为c，月球绕地球及卫星绕月球均做匀速圆周运动。求：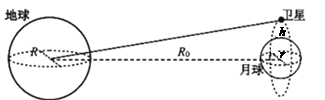
（1）地球的质量M和月球的质量m及月球的第一宇宙速度v；
（2）如图所示，当绕月球地轨道的平面与月球绕地球公转的轨道平面垂直（即与地心到月心的连线垂直）时，绕月球地卫星向地球地面发送照片需要的最短时间t。
如图所示，水平传送带水平段长l=3m，两皮带轮半径均为r =5cm，距地面高度h=3.2m，此时传送带静止。与传送带等高的光滑平台上，有一个可看成质点的小物体以v0的初速度滑上传送带，从传送带的右端飞出做平抛运动，水平射程是1.6m。已知物块与传送带间的动摩擦因数为0.2，g=10m/s2。求：
（1）物体的初速度
；
（2）保持其它条件不变，为使物块作平抛运动的水平射程最大，则皮带轮至少应以多大的角速度转动？
一物块以一定的初速度沿斜面向上滑出，利用速度传感器可以在计算机屏幕上得到其速度大小随时间的变化关系如图所示，g=10m/s2。求：
（1）物块上滑和下滑的加速度大小a1、a2，及向上滑行的最大距离x；
（2）斜面的倾角θ及物块与斜面间的动摩擦因数μ。
发射地球同步卫星时，可认为先将卫星发射至距地面高度为h1的圆形轨道上，在卫星经过A点时点火（喷气发动机工作）实施变轨进入椭圆轨道，椭圆轨道的近地点为A，远地点为B。在卫星沿椭圆轨道运动经过B点再次点火实施变轨，将卫星送入同步轨道（远地点B在同步轨道上），如图所示。两次点火过程都是使卫星沿切向方向加速，并且点火时间很短。已知同步卫星的运动周期为T，地球的半径为R，地球表面重力加速度为g，求
（1）地球的第一宇宙速度；
（2）卫星在圆形轨道运行接近A点时的加速度大小；
（3）卫星同步轨道距地面的高度。
几位同学探究“用圆锥摆粗略验证向心力的表达式”。他们用细线吊着一小铁球，使小铁球在水平面内做匀速圆周运动，如图。他们用仪器测出下列物理量：小铁球质量m，悬点O到球心距离L，细线与竖直方向的夹角α。已知重力加速度为g。求：
（1）小铁球做匀速圆周运动时向心力的大小；
（2）小铁球做匀速圆周运动时的角速度；
（3）小铁球做匀速圆周运动时的线速度。
粤公网安备 44130202000953号