一球形人造卫星,其最大横截面积为A、质量为m,在轨道半径为R的高空绕地球做圆周运动。由于受到稀薄空气阻力的作用,导致卫星运行的轨道半径逐渐变小。卫星在绕地球运转很多圈之后,其轨道的高度下降了△H,由于△H <<R,所以可以将卫星绕地球运动的每一圈均视为匀速圆周运动。设地球可看成质量为M的均匀球体,万有引力常量为G。取无穷远处为零势能点,当卫星的运行轨道半径为r时,卫星与地球组成的系统具有的势能可表示为 。
。
(1)求人造卫星在轨道半径为R的高空绕地球做圆周运动的周期;
(2)某同学为估算稀薄空气对卫星的阻力大小,做出了如下假设:卫星运行轨道范围内稀薄空气的密度为ρ,且为恒量;稀薄空气可看成是由彼此不发生相互作用的颗粒组成的,所有的颗粒原来都静止,它们与人造卫星在很短时间内发生碰撞后都具有与卫星相同的速度,在与这些颗粒碰撞的前后,卫星的速度可认为保持不变。在满足上述假设的条件下,请推导:
①估算空气颗粒对卫星在半径为R轨道上运行时,所受阻力F大小的表达式;
②估算人造卫星由半径为R的轨道降低到半径为R-△H的轨道的过程中,卫星绕地球运动圈数n的表达式。
、宇航员登上某一星球并在该星球表面做实验,用一根不可伸缩的轻绳跨过轻质定滑轮,一端挂一吊椅,另一端被坐在吊椅上的宇航员拉住,如图所示。宇航员的质量m1=65kg,吊椅的质量m2=15kg,当宇航员与吊椅以a=1m/s2的加速度匀加速上升时,宇航员对吊椅的压力为l75N。(忽略定滑轮摩擦)
(1)求该星球表面的重力加速度g;
(2)若该星球的半径R=6×106m,地球半径R0=6.4×106m,地球表面的重力加速度g0=10m/s2,求该星球的平均密度与地球的平均密度之比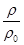 。
。
试将一天的时间记为T,地球半径记为R,地球表面重力加速度为g.(结果可保留根式)
(1)试求地球同步卫星P的轨道半径RP;
(2)若已知一卫星Q位于赤道上空且卫星Q运动方向与地球自转方向相反,赤道上一城市A的人平均每三天观测到卫星Q四次掠过他的上空,试求Q的轨道半径RQ
天文学家将相距较近,仅在彼此的引力作用填运行的两颗恒星称为双星,双星系统在银河系中很普遍,利用双星系统中两颗恒星的运动特征可推算出它们的总质量,已知某双星系统中两颗恒星围绕它们连线上的某一点分别做匀速圆周运动,周期均为T,两颗恒星之间的距离为r,万有引力常量为G,试推算这个双星系统的总质量
2013年6月,我国成功实现目标飞行器“神舟十号”与轨道空间站“天宫一号”的对接.如图所示,已知“神舟十号”从捕获“天宫一号”到实现对接用时t,这段时间内组合体绕地球转过的角度为θ(此过程轨道不变,速度大小不变),地球半径为R,地球表面重力加速度为g,万有引力恒量G,不考虑地球自转;求: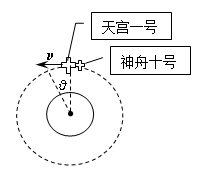
(1)地球质量M;
(2)组合体运动的周期T;
(3)组合体所在圆轨道离地高度H。
某宇航员在一星球表面附近高度为H处以速度v0水平抛出一物体,经过一段时间后物体落回星球表面,测得该物体水平位移为x,已知星球半径为R,万有引力常量为G.不计空气阻力,求:
(1)该星球质量M;
(2)该星球第一宇宙速度大小v.
如图所示,双星系统中的星球A、B都可视为质点,A、B绕两者连线上的O点做匀速圆周运动,A、B之间距离不变,引力常量为G,观测到A的速率为v、运行周期为T,A、B的质量分别为mA、mB.
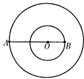
(1)求B的周期和速率.
(2)A受B的引力FA可等效为位于O点处质量为m′的星体对它的引力,试求m′.(用mA、mB表示)( )
由于地球自转的影响,地球表面的重力加速度会随纬度的变化而有所不同:若地球表面两极处的重力加速度大小为g0,在赤道处的重力加速度大小为g,地球自转的周期为r,引力常量为G,地球可视为质量均匀分布的球体.求:
(1)地球半径R;
(2)地球的平均密度;
(3)若地球自转速度加快,当赤道上的物体恰好能“飘”起来时,求地球自转周期T'.
黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成。两星视为质点,不考虑其它天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示。引力常量为G,由观测能够得到可见星A的速率v和运行周期T。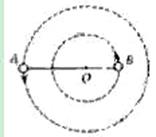
(1)可见星A所受暗星B的引力 可等效为位于O点处质量为
可等效为位于O点处质量为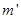 的星体(视为质点)对它的引力,设A和B的质量分别为
的星体(视为质点)对它的引力,设A和B的质量分别为 、
、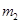 ,试求
,试求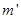 (用
(用 、
、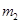 表示);
表示);
(2)求暗星B的质量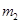 与可见星A的速率v、运行周期T和质量
与可见星A的速率v、运行周期T和质量 之间的关系式;
之间的关系式;
(3)恒星演化到末期,如果其质量大于太阳质量 的2倍,它将有可能成为黑洞。若可见星A的速率v=2.7×105m/s,运行周期T=4.7π×104s,质量m1=6
的2倍,它将有可能成为黑洞。若可见星A的速率v=2.7×105m/s,运行周期T=4.7π×104s,质量m1=6 ,试通过估算来判断暗星B有可能是黑洞吗?(G=6.67×10-11N·m2/kg2,ms=2.0×1030kg)
,试通过估算来判断暗星B有可能是黑洞吗?(G=6.67×10-11N·m2/kg2,ms=2.0×1030kg)
在勇气号火星探测器着陆的最后阶段,着陆器降落到火星表面上,再经过多次弹跳才停下来。假设着陆器第一次落到火星表面弹起后,到达最高点时高度为h,速度方向是水平的,速度大小为v0,求它第二次落到火星表面时速度的大小,计算时不计火星大气阻力。已知火星的一个卫星的圆轨道的半径为r,周期为T,火星可视为半径为r0的均匀球体。
阅读以下信息:
①2013年12月2日1时30分,“嫦娥三号”在西昌卫星发射中心发射,经过19分钟的飞行后,火箭把“嫦娥三号”送入近地点高度210千米、远地点高度约36.8万千米的地月转移轨道。“嫦娥三号”奔月的近似轨迹如图所示。
②经过地月转移轨道上的长途飞行后,“嫦娥三号”在距月面高度约100千米处成功变轨,进入环月圆轨道。在该轨道上运行了约4天后,再次成功变轨,进入近月点高度15千米、远月点高度100千米的椭圆轨道。
③2013年12月14日晚21时,随着首次应用于中国航天器的空间变推力发动机开机,沿椭圆轨道通过近月点的“嫦娥三号”从每秒钟1.7千米的速度实施动力下降。
④2013年12月14日21时11分,“嫦娥三号”成功实施软着陆。
⑤开普勒行星运动第三定律指出:行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比,即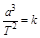 ,k是一个对所有行星都相同的常量。该定律适用于一切具有中心天体的引力系统。
,k是一个对所有行星都相同的常量。该定律适用于一切具有中心天体的引力系统。
⑥月球的质量M=7.35×1022kg,半径R=1.74×103km;月球绕地球运行的轨道半长轴a0=3.82×105km,月球绕地球运动的周期T0=27.3d(d表示天);质量为m的物体在距离月球球心r处具有的引力势能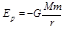 ,引力常量G=6.67×10-11 N·m2/kg2;地球的半径R0=6.37×103km。
,引力常量G=6.67×10-11 N·m2/kg2;地球的半径R0=6.37×103km。
根据以上信息,请估算: 
(1)“嫦娥三号”在100km环月圆轨道上运行时的速率v;
(2)“嫦娥三号”在椭圆轨道上通过远月点时的速率v远;
有些航空母舰上装有帮助飞机起飞的弹射系统,已知某型号的舰载飞机在跑道上加速时可能产生的最大加速度为5m/s2,当飞机的速度达到50m/s时才能离开航空母舰起飞,设航空母舰处于静止状态.问:
(1)若要求该飞机滑行160m后起飞,弹射系统必须使飞机具有多大的初速度?
(2)若航空母舰上不装弹射系统,设航空母舰甲板长为L=160m,为使飞机仍能此舰上正常起飞,这时可以先让航空母舰沿飞机起飞方向以某一速度匀速航行,则这个速度至少为多少?
(12分)“嫦娥工程”计划在第二步向月球发射一个软着陆器,在着陆器附近进行现场勘测.已知地球的质量约为月球质量的80倍,地球的半径约为月球半径的4倍,地球表面的重力加速度为g地=10m/s2,地球的第一宇宙速度为7.9km/s。假设将来测得着陆器撞击月球表面后又竖直向上弹起,并且经过2s钟后落回到月球表面.试求:(1)它弹起时的初速度v0。(2)月球的第一宇宙速度是多少。(不考虑地球和月球的自转;结果保留两位有效数字).
(15分)我国发射的“嫦娥一号”卫星发射后首先进入绕地球运行的“停泊轨道”,通过加速再进入椭圆“过渡轨道”,该轨道离地心最近距离为L1,最远距离为L2,卫星快要到达月球时,依靠火箭的反向助推器减速,被月球引力“俘获”后,成为环月球卫星,最终在离月心距离L3的“绕月轨道”上飞行,如图所示.已知地球半径为R,月球半径为r,地球表面重力加速度为g,月球表面的重力加速度为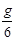 ,求:
,求: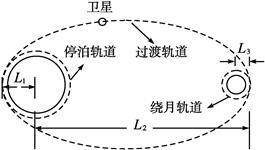
(1)卫星在“停泊轨道”上运行的线速度大小;
(2)卫星在“绕月轨道”上运行的线速度大小;
(3)假定卫星在“绕月轨道”上运行的周期为T,卫星轨道平面与地月连心线共面,求在该一个周期内卫星发射的微波信号因月球遮挡而不能到达地球的时间(忽略月球绕地球转动对遮挡时间的影响).