高中物理万有引力定律及其应用计算题

如图所示，“神舟”十号宇宙飞船控制中心的大屏幕上出现的一幅卫星运行轨迹图，它记录了飞船在地球表面垂直投影的位置变化；图中表示在一段时间内飞船绕地球圆周飞行四圈，依次飞经中国和太平洋地区的四次轨迹①、②、③、④，图中分别标出了各地点的经纬度（如：在轨迹①通过赤道时的经度为西经157.5°，绕行一圈后轨迹②再次经过赤道时经度为180°……），若地球质量为M，地球半径为R，万有引力恒量为G 。请完成以下问题：

①飞船轨道平面与赤道平面的夹角为                ；
②飞船绕地球运行的周期（写出分析原因及计算过程）
③飞船运行轨道距地球表面的高度（写出计算过程）。

宇宙飞船以a=g/2的加速度匀加速上升，由于超重现象，用弹簧秤测得质量为10kg的物体重量为75N，由此可求飞船所处位置距地面高度为多少？(地球半径R=6400km,g=10m/s²)

宇航员在地球表面以一定初速度竖直上抛一小球，经过时间t小球落回原处；若他在某星球表面以相同的初速度竖直上抛同一小球，需经过时间5t小球落回原地．(取地球表面重力加速度g＝10 m/s²，阻力不计)
(1)求该星球表面附近的重力加速度g′；
(2)已知该星球的半径与地球半径之比为R_星∶R_地＝1∶4，求该星球的质量与地球质量之比M_星∶M_地．

已知“天宫一号”在地球上空的圆轨道上运行时离地面的高度为h，地球半径为R，地球表面的重力加速度为g．求：
（1）地球的密度为多少
（2）“天宫一号”在该圆轨道上运行时速度v的大小；

、宇航员登上某一星球并在该星球表面做实验，用一根不可伸缩的轻绳跨过轻质定滑轮，一端挂一吊椅，另一端被坐在吊椅上的宇航员拉住，如图所示。宇航员的质量m₁=65kg，吊椅的质量m₂=15kg，当宇航员与吊椅以a=1m/s²的加速度匀加速上升时，宇航员对吊椅的压力为l75N。(忽略定滑轮摩擦)

（1）求该星球表面的重力加速度g；
（2）若该星球的半径R=6×10⁶m，地球半径R₀=6.4×10⁶m，地球表面的重力加速度g₀=10m/s²，求该星球的平均密度与地球的平均密度之比。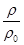

两颗人造地球卫星的质量之比轨道半径之比，那么，它们的周期之比__________，它们所受向心力之比__________。

2012年4月30日4时50分，我国在西昌卫星发射中心用“长征三号乙”运载火箭首次采用“一箭双星”的方式，成功发射两颗北斗导航卫星，卫星顺利进入预定转移轨道．北斗卫星导航系统是中国自行研制开发的区域性有源三维卫星定位与通信系统（CNSS），其空间端包括5颗静止轨道卫星和30颗非静止轨道卫星，如图甲所示， 为简便起见，认为其中一颗卫星轨道平面与地球赤道平面重合，绕地心做匀速圆周运动（如图乙所示）．已知地球表面重力加速度为g，地球的半径R，该卫星绕地球匀速圆周运动的周期为T，求该卫星绕地球作匀速圆周运动的轨道半径r．

2008年9月27日，“神舟七号”航天员翟志刚首次实现了中国航天员在太空的舱外活动（如图），这是我国航天发展史上的又一里程碑. 已知引力常量为G，地球质量为M，地球半径为R. 飞船绕地球做匀速圆周运动的过程中，距地面的高度为h，求：（1）飞船加速度a的大小；
（2）飞船速度v的大小.

某颗人造地球卫星在距地面高度为h的圆形轨道上绕地球飞行，其运动可视为匀速圆周运动。已知地球半径为R，地面附近的重力加速度为g。求：
（1）卫星在圆形轨道上运行速度的表达式；
（2）卫星在圆形轨道上运行周期的表达式。

“神舟十号”飞船在绕地球做匀速圆周运动时，离地面的高度为h，周期为T，已知地球的半径为R，引力常量为G，写出地球质量和密度的表达式。

宇航员驾驶宇宙飞船到达月球，他在月球表面做了一个实验：在离月球表面高度为h处，将一小球以初速度v₀水平抛出，水平射程为x。已知月球的半径为R，万有引力常量为G。不考虑月球自转的影响。求：
（1）月球表面的重力加速度大小g₀ ；
（2）月球的质量M；
（3）飞船在近月圆轨道绕月球做匀速圆周运动的速度v。

在勇气号火星探测器着陆的最后阶段，着陆器降落到火星表面上，再经过多次弹跳才停下来．假设着陆器第一次落到火星表面弹起后，到达最高点时的高度为h，速度方向是水平的，速度大小为v₀，求它第二次落到火星表面时速度的大小，计算时不计火星大气阻力．已知火星的一个卫星的圆轨道的半径为r，周期为T．火星可视为半径为r₀的均匀球体．

天文学家将相距较近，仅在彼此的引力作用填运行的两颗恒星称为双星，双星系统在银河系中很普遍，利用双星系统中两颗恒星的运动特征可推算出它们的总质量，已知某双星系统中两颗恒星围绕它们连线上的某一点分别做匀速圆周运动，周期均为T，两颗恒星之间的距离为r，万有引力常量为G，试推算这个双星系统的总质量

地球绕太阳公转的轨道半径为1.49×10¹¹m，公转的周期是3.16×10⁷s，太阳的质量是多少？（已知万有引力常数G=6.67×10^-11Nm²/kg²）（计算结果保留1位有效数字）

质量为m的卫星离地面R₀处做匀速圆周运动。设地球的半径也为R₀，地面的重力加速度为g，引力常数G，求：（1）地球的质量； （2）卫星的线速度大小。