高中物理匀速圆周运动综合题

如图所示，在匀速转动的水平圆盘上，沿半径方向放置两个用细线相连的质量均为m的小物体A、B，它们到转轴的距离分别为r_A="20" cm，r_B="30" cm，A、B与盘面间最大静摩擦力均为重力的0.4倍，试求：
（1）当细线上开始出现张力时，圆盘的角速度；
（2）当A开始滑动时，圆盘的角速度；
（3）当A即将滑动时，烧断细线，A、B运动状态如何？(g取10 m/s²)

如图所示，有一根长为2L的轻质细线，它的两端固定在一根长为L的竖直转轴AB上，线上套一个可以自由移动的质量为m的小球。当转轴转动时，小球正好以B为圆心，在水平面内做匀速圆周运动。求细线的张力和小球的线速度。

（1）、飞船正常运行时的速度V的表达式及数值；
（2）、飞船在圆轨道上运行的周期T。

求 ．

“一个周末的傍晚，你爸爸终于有了时间，带着你们全家驱车以速度V₀行驶来到你向往已久的乡野．你们正尽情地享受着乡野迷人的气息，突然你眼前一亮，车灯照亮了一片水波！你大声惊呼地闭上了眼……”同学们不用紧张，这只是编的一个故事．
假设车灯照亮的是一条垂直于汽车行驶方向小河沟，车的周围是一片平地。你爸爸选择立即刹车（设刹车时汽车做匀减速直线运动），使车恰好停在河边而逃过一劫；或选择立即拐弯（设拐弯时汽车做匀速圆周运动)，是否能幸免一难？（可借助V₀、g、μ等物理量表达结论）

已知地球半径R ＝6.4×10⁶m，地面附近重力加速度g ="9.8" m/s2，计算在距离地面高为h＝2×10⁶m的圆形轨道上的卫星做匀速率圆周运动的线速度v和周期T.

继神秘的火星之后，今年土星也成了全世界关注的焦点！经过近7年35.2亿公里在太空中风尘仆仆的穿行后，美航空航天局和欧航空航天局合作研究的“卡西尼”号土星探测器于美国东部时间6月30日（北京时间7月1日）抵达预定轨道，开始“拜访”土星及其卫星家族。这是人类首次针对土星及其31颗已知卫星最详尽的探测！若“卡西尼”号探测器进入绕土星飞行的轨道，在半径为R的土星上空离土星表面高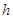的圆形轨道上绕土星飞行，环绕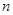周飞行时间为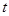。试计算土星的质量和平均密度。

如图，长为L的不可伸长的细线，拴一质量为m的小球，一端固定于O点，让其在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动)，如图所示。当摆线L与竖直方向的夹角是α时，求：
(1)线的拉力F；
(2)小球运动的周期。

提示：1．黑洞是一种密度极大的天体，其表面的引力是如此之强，以致包括光在内的所有物质都逃脱不了其引力的作用。
2．计算中可以采用拉普拉斯黑洞模型，在这种模型中，在黑洞表面上的所有物质，即使初速度等于光速c也逃脱不了其引力的作用。（光速c=3×10⁸m/s）

如图5-4-9所示是生产流水线上的皮带传输装置，传输带上等间距地放着很多半成品产品.A轮处装有光电计数器，它可以记录通过A处的产品数目，已经测得轮A、B的半径分别为r_A="20" cm、r_B="10" cm，相邻两产品距离为30 cm，1分钟内有41个产品通过A处（即从第一个产品到A处开始计时直至第四十一个产品到A处），求：

图5-4-9
（1）产品随传送带移动的速度大小；
（2）A、B轮轮缘上的两点P、Q及A轮半径中点M的线速度和角速度大小；
（3）如果A轮是通过摩擦带动C轮转动，且r_c="5" cm，求出C轮的角速度（轮不打滑）.

一卫星绕某行星做匀速圆周运动，已知行星表面的重力加速度为ｇ_行，行星的质量Ｍ与卫星的质量ｍ之比Ｍ／ｍ＝81，行星的半径Ｒ_行与卫星的半径Ｒ_卫之比Ｒ_行／Ｒ_卫＝3.6，行星与卫星之间的距离ｒ与行星的半径Ｒ_行之比ｒ／Ｒ_行＝60。设卫星表面的重力加速度为ｇ_卫，则在卫星表面有：ＧＭｍ／ｒ^２＝ｍｇ_卫　……
　经过计算得出：卫星表面的重力加速度为行星表面的重力加速度的1/3600。上述结果是否正确?若正确，列式证明；若错误，求出正确结果。

如图光滑的水平面上钉有两枚铁钉A和B，相距0.1m，长1m的柔软细绳拴在A上，另一端系一质量为0.5kg的小球，小球的初始位置在AB连线上A的一侧，把细线拉紧，给小球以2m/s的垂直细线方向的水平速度使它做圆周运动，由于钉子B的存在，使线慢慢地缠在A、B上．如果细线的抗断拉力为7N，从开始运动到细线断裂需经历多长时间?