如图所示,AB为竖直半圆轨道的竖直直径,轨道半径R=0.9m,轨道B端与水平面相切,质量m=1kg的光滑小球从水平面以初速度V0向B滑动,取g=10m/s2。
(1)若V0=6m/s,求小球经轨道最低点B瞬间对轨道的压力为多少?
(2)若小球刚好能经过A点,则小球在A点的速度至少为多大?小球离开A点后在水平面的落点与B点的距离为多少?
如图所示,将一个小球水平抛出,抛出点距水平地面的高度h=1.8m,小球抛出的初速度为 。不计空气阻力。取g=
。不计空气阻力。取g= 。求:
。求:
(1)小球从抛出到落地经历的时间t;
(2)小球落地点与抛出点的水平距离S;
(3)小球落地时的速度大小V。
如图所示,装甲车在水平地面上以速度沿直线前进,车上机枪的枪管水平,距地面高为
。在车正前方竖直一块高为两米的长方形靶,其底边与地面接触。枪口与靶距离为
时,机枪手正对靶射出第一发子弹,子弹相对于枪口的初速度为
。在子弹射出的同时,装甲车开始匀减速运动,行进
后停下。装甲车停下后,机枪手以相同方式射出第二发子弹。(不计空气阻力,子弹看成质点,重力加速度
)

(1)求装甲车匀减速运动时的加速度大小;
(2)当时,求第一发子弹的弹孔离地的高度,并计算靶上两个弹孔之间的距离;
(3)若靶上只有一个弹孔,求的范围。
如图,、
、
为同一竖直平面内的三个点,
沿竖直方向,
,
.将一质量为
的小球以一定的初动能自
点水平向右抛出,小球在运动过程中恰好通过
点。使此小球带电,电荷量为
(
>0),同时加一匀强电场,场强方向与
所在平面平行,现从
点以同样的初动能沿某一方向抛出此带点小球,该小球通过了
点,到达
点时的动能是初动能的3倍;若该小球从
点以同样的初动能沿另一方向抛出,恰好通过
点,且到达
点的动能为初动能的6倍,重力加速度大小为
。求

(1)无电场时,小球达到点时的动能与初动能的比值;
(2)电场强度的大小和方向。
图为某游乐场内水上滑梯轨道示意图,整个轨道在同一竖直平面内,表面粗糙的段与四分之一光滑圆弧轨道
在
点水平相切。点
距水面的高度为H,圆弧轨道BC的半径为R,圆心
恰在水面。一质量为
的游客(视为质点)可从轨道
的任意位置滑下,不计空气阻力。

(1)若游客从点由静止开始滑下,到
点时沿切线方向滑离轨道落在水面
点,
,求游客滑到的速度
大小及运动过程轨道摩擦力对其所做的功
;
(2)若游客从段某处滑下,恰好停在
点,有因为受到微小扰动,继续沿圆弧轨道滑到
点后滑离轨道,求
点离水面的高度
。(提示:在圆周运动过程中任一点,质点所受的向心力与其速率的关系为
)
如图所示,质量为m=1kg的小球用线长l=1m的细线拴住,细绳上端固定在O点,当小球从图示M点释放后摆到悬点O的正下方N点时,细线恰好被拉断,此后小球刚好能无碰撞地从置于地面上倾角为45º的斜面滑下,已知斜面高度 h=0.4m,斜面左端离O点正下方的P点水平距离S=0.4m,不计空气阻力,求:

(1)N点距离地面的高度H
(2)细绳能承受的最大拉力
如图所示,一个小球以v0=8.0 m/s速度从圆弧轨道的O点水平抛出,恰好能沿着斜面所在的方向落在Q点。已知斜面光滑,斜面与水平面的夹角为θ=37°,斜面的高度为h=15 m.忽略空气阻力的影响,重力加速度为g=10 m/s2。求小球从O点抛出到斜面底端的M点所用的总时间。(保留两位有效数字)
一艘客轮因故障需迅速组织乘客撤离。乘客在甲板上须利用固定的绳索下滑到救援快艇上。绳索与竖直方向的夹角θ=37°,设乘客下滑过程绳索始终保持直线。为保证行动又快又安全,乘客先从静止开始匀加速滑到某最大速度,再匀减速滑至快艇,速度刚好为零,加速过程与减速过程中的加速度大小相等。在乘客开始下滑时,船员同时以水平速度 向快艇抛出救生圈刚好落到救援快艇上(快艇可视为质点),如图所示。并知乘客下滑的时间是救生圈平抛下落的2倍,不计空气阻力,重力加速度g取10 m/s2,sin37°= 0.6,cos37°= 0.8,求:
向快艇抛出救生圈刚好落到救援快艇上(快艇可视为质点),如图所示。并知乘客下滑的时间是救生圈平抛下落的2倍,不计空气阻力,重力加速度g取10 m/s2,sin37°= 0.6,cos37°= 0.8,求:
(1)乘客沿着绳索下滑的时间t;
(2)乘客下滑过程的最大速度vm。
分 如图所示,平台上的小球从A点水平抛出,恰能无碰撞地进入光滑的BC斜面,经C点进入光滑平面CD时速率不变,最后进入悬挂在O点并与水平面等高的弧形轻质筐内。已知小球质量为1kg,A、B两点高度差2m,BC斜面高4m,倾角 ,悬挂弧筐的轻绳长为6m,小球看成质点,轻质筐的重量忽略不计,弧形轻质筐的大小远小于悬线长度,重力加速度为g=10m/s2 ,试求:
,悬挂弧筐的轻绳长为6m,小球看成质点,轻质筐的重量忽略不计,弧形轻质筐的大小远小于悬线长度,重力加速度为g=10m/s2 ,试求:
(1)B点与抛出点A的水平距离x;
(2)小球运动至C点的速度 大小;
大小;
(3)小球进入轻质筐后瞬间,小球所受拉力F的大小.
一人用一根长L=1m,最大只能承受T=46N拉力的轻绳子,拴着一个质量m=1kg的小球(不考虑其大小),在竖直平面内作圆周运动,已知圆心O离地高H=21m,如图所示,若小球运动到达最低点时绳刚好被球拉断,求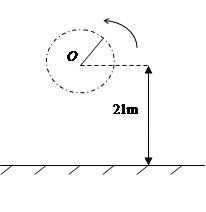
(1)小球到达最低点的速度大小是多少?
(2)小球落地点到O点的水平距离是多少?(g=10m/s2)
)如图所示,某人骑摩托车在水平道路上行驶,要在A处越过x=5m的壕沟,沟面对面比A处低h=1.25m,(取g=10m/s2)求:
(1)摩托车在空中飞行的时间?
(2)摩托车的开始飞越壕沟的初速度至少要有多大?
如图所示,轨道ABCD的AB段为一半径R=0.2 的光滑1/4圆形轨道,BC段为高为h=5
的光滑1/4圆形轨道,BC段为高为h=5 的竖直轨道,CD段为水平轨道。一质量为0.1
的竖直轨道,CD段为水平轨道。一质量为0.1 的小球由A点从静止开始下滑到B点时速度的大小为2
的小球由A点从静止开始下滑到B点时速度的大小为2 /s,离开B点做平抛运动(g取10
/s,离开B点做平抛运动(g取10 /s2),求:
/s2),求:
(1)小球离开B点后,在CD轨道上的落地点到C的水平距离
(2)小球到达B点时对圆形轨道的压力;
(3)如果在BCD轨道上放置一个倾角 =45°的斜面(如图中虚线所示),那么小球离开B点后能否落到斜面上?如果能,求它第一次落在斜面上的位置。
=45°的斜面(如图中虚线所示),那么小球离开B点后能否落到斜面上?如果能,求它第一次落在斜面上的位置。
如图所示,一小球从平台上水平抛出,恰好落在临近平台的一倾角为α=53°的光滑斜面顶端,并刚好沿光滑斜面下滑,已知斜面顶端与平台的高度差h=0.8 m,g=10 m/s2,sin 53°=0.8,cos 53°=0.6,则:
(1)小球水平抛出的初速度v0是多大?
(2)斜面顶端与平台边缘的水平距离x是多少?
(3)若斜面顶端高H=20.8 m,则小球离开平台后经多长时间t到达斜面底端?
如图所示在倾角为37°的斜面上,从A点以20 m/s的初速度水平抛出一个小球,小球落在B点。求小球在空中飞行的时间t和A、B两点间的距离s.(g=10 m/s2,sin 37°=0.6,cos 37°=0.8)