高中物理力的分解计算题

用重力可以忽略不计的细绳将镜框悬挂在一面竖直墙上，如图所示。细绳AO、BO与镜框共面，且两段细绳与镜框上边沿的夹角均为60⁰。已知镜框重力为G，镜框上边沿水平，求细绳AO、BO所受拉力大小。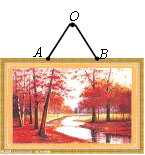

如图(a)所示，轻绳AD跨过固定在水平横梁BC右端的定滑轮挂住一个质量为M₁的物体，∠ACB＝30°；如图(b)中轻杆HG一端用铰链固定在竖直墙上，另一端G通过细绳EG拉住，EG与水平方向也成30°，轻杆的G点用细绳CF拉住一个质量为M₂的物体，求：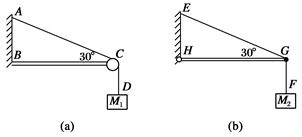

(1)细绳AC段的张力T_AC与细绳EG的张力T_EG之比；
(2)轻杆BC对C端的支持力；
(3)轻杆HG对G端的支持力．

有些人，像电梯修理员、牵引专家和赛艇运动员，常需要知道绳或金属线中的张力，可又不能到那些绳、线的自由端去测量．一家英国公司现在制造出一种夹在绳上的仪表，用一个杠杆使绳子的某点有一个微小偏移量，如图所示，仪表很容易测出垂直于绳的恢复力．推导一个能计算绳中张力的公式．如果偏移量为12 mm，恢复力为300 N，计算绳中张力．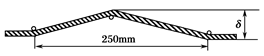

如图所示，能承受最大拉力为10 N的细线OA与竖直方向成45°角，能承受最大拉力为5 N的细线OB水平，细线OC能承受足够的拉力，为使OA、OB均不被拉断，OC下端所悬挂物体的最大重力是多少？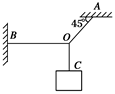

如图所示，杆OA长为R，可绕过O点的水平轴在竖直平面内转动，其端点A系   着一跨过定滑轮B、C的不可伸长的轻绳，绳的另一端系一物块M，滑轮的半径可忽略，B在O的正上方，OB之间的距离为H。某一时刻，当绳的BA段与OB之间的夹角为α＝30°时，杆的角速度为ω，求此时物块M的速率 v_M。

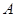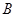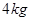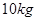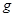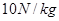如图13所示,物体、质量分别是和,不计滑轮与绳间摩擦及绳的重力,若整个系统静止,取。求：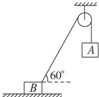
     
（1）地面对B的摩擦力的大小；
（2）地面对B支持力的大小。

如图所示，用绳AC和BC吊起一个物体，绳AC与竖直方向的夹角为60°，绳BC与竖直方向的夹角为30°。若被吊起的物体重100N，试求绳AC和BC中张力分别为多大?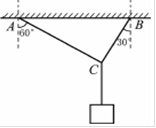

如图所示，用细绳将重球悬挂在光滑墙壁上，绳子与墙夹角为θ，球的重力为G。

（1）用力的分解法则作出重力和重力沿绳子方向及垂直墙壁方向的两个分力
（2）这两个分力的大小是多大？

如图所示，一只小球用绳OA和OB拉住，OA水平，OB与水平方向成60°角，这时OB绳受的拉力为8 N，求小球重力及OA绳拉力的大小．

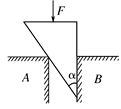
刀、斧、凿、刨等切削工具的刃都叫做劈，劈的截面是一个等腰三角形，如图所示，使用劈的时候，在劈背上加力F，这个力产生的作用效果是使劈的两侧面推压物体，把物体劈开.设劈的纵截面是一个等腰三角形，劈背的宽度是d，劈的侧面的长度是L.通过计算说明为什么劈的两个侧面之间的夹角越小（即越锋利的切削工具）越容易劈开物体。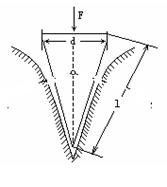

如图所示，斜面倾角为θ=37⁰，在斜面上放着一重为100N的物体，问：

⑴ 重力沿斜面下滑方向的分力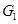、沿斜面垂直方向的分力各多大？
⑵ 如果物体和斜面间的动摩擦因数为0.2，那么让物体下滑，在下滑过程中物体受到的摩擦力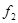多大？方向如何？（sin37⁰=0.6，cos37⁰=0.8）

一个质量为m、电量为+q的小球，用丝线悬挂在水平方向的匀强电场中，场强为E，平衡时悬线与竖直方向间夹角α="30" °(如图所示)，若将匀强电场E的方向逆时针转过角度β=45°，小球重新平衡时悬线与竖直方向间夹角正切为多大?（可以保留根号）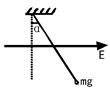

如图所示，倾角为θ的固定斜面上有一质量为m的物体，物体与斜面的动摩擦因数为μ，当受一水平推力F作用时，求:为使物体匀速上滑则F应为多大?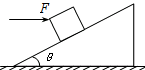

如图，轻绳OA一端系在天花板上，与竖直线夹角37°，轻绳OB水平，一端系在墙上，O点处挂一重为40N的物体．（cos37°="0.8," sin37°=0.6） 求OA、OB的拉力各为多大？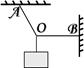

如图所示，表面光滑、质量不计的尖劈，插在缝A、B之间，尖劈的一个角为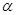，在尖劈背上加一压力F，则尖劈对A侧压力和对B侧压力分别为多大？（在图上画出力的示意图）