竖直面内一倾斜轨道与一足够长的水平轨道通过一小段光滑圆弧平滑连接,小物块B静止于水平轨道的最左端,如图(a)所示。
时刻,小物块A在倾斜轨道上从静止开始下滑,一段时间后与B发生弹性碰撞(碰撞时间极短);当A返回到倾斜轨道上的P点(图中未标出)时,速度减为0,此时对其施加一外力,使其在倾斜轨道上保持静止。物块A运动的
图像如图(b)所示,图中的
和
均为未知量。已知A的质量为m,初始时A与B的高度差为H,重力加速度大小为g,不计空气阻力。
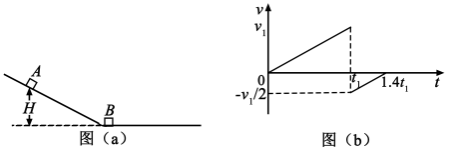
(1)求物块B的质量;
(2)在图(b)所描述的整个运动过程中,求物块A克服摩擦力所做的功;
(3)已知两物块与轨道间的动摩擦因数均相等,在物块B停止运动后,改变物块与轨道间的动摩擦因数,然后将A从P点释放,一段时间后A刚好能与B再次碰上。求改变前面动摩擦因数的比值。
(1)用一个摆长为 的单摆做实验,要求摆动的最大角度小于 ,则开始时摆球拉离平衡位置的距离应不超过 (保留1位小数)。(提示:单摆被拉开小角度的情况下,所求的距离约等于摆球沿圆弧移动的路程。 某同学想设计一个新单摆,要求新单摆摆动10个周期的时间与原单摆摆动11个周期的时间相等。新单摆的摆长应该取为 。
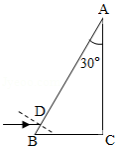
(2)直角棱镜的折射率 ,其横截面如图所示,图中 , .截面内一细束与 边平行的光线,从棱镜 边上的 点射入,经折射后射到 边上。
光线在 边上是否会发生全反射?说明理由;
不考虑多次反射,求从 边射出的光线与最初的入射光线夹角的正弦值。
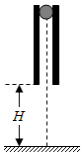
如图,一竖直圆管质量为 ,下端距水平地面的高度为 ,顶端塞有一质量为 的小球。圆管由静止自由下落,与地面发生多次弹性碰撞,且每次碰撞时间均极短;在运动过程中,管始终保持竖直。已知 ,球和管之间的滑动摩擦力大小为 , 为重力加速度的大小,不计空气阻力。
(1)求管第一次与地面碰撞后的瞬间,管和球各自的加速度大小;
(2)管第一次落地弹起后,在上升过程中球没有从管中滑出,求管上升的最大高度;
(3)管第二次落地弹起的上升过程中,球仍没有从管中滑出,求圆管长度应满足的条件。
某游乐园入口旁有一喷泉, 喷出的水柱将一质量为 的卡通玩具稳定地悬停在 空中。为计算方便起见,假设水柱从横截面积为 的喷口持续以速度 v0 竖直向上喷出; 玩具 底部为平板(面积略大于 ); 水柱冲击到玩具底板后, 在竖直方向水的速度变为零, 在水平方向朝四周均匀散开。忽略空气阻力。已知水的密度为 , 重力加速度大小为 求
(i) 喷泉单位时间内喷出的水的质量;
(ii)玩具在空中悬停时, 其底面相对于喷口的高度。
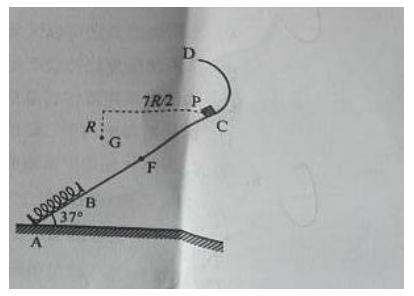
如图, 一轻弹簧原长为 , 其一端固定在倾角为 的固定直轨道 的底端 处, 另一端位于直轨道上 处, 弹簧处于自然状态, 直轨道与一半径为 的光滑圆弧轨道相切于 点, 均在同一竖直面内。质量为 的小物块 自 点由静止开 始下滑, 最低到达 点(末画出 , 随后 沿轨道被弹回, 最高点到达 点, , 已知
与直轨道间的动摩擦因数 , 重力加速度大小为 (取 )
(1) 求 P 第一次运动到 点时速度的大小。
(2) 求 运动到 点时弹簧的弹性势能。
(3) 改变物块 的质量, 将 推至 点, 从静止开始释放。已知 自圆弧轨道的最高点 处水平飞出后, 恰好通过 点。 点在 点左下方,与 点水平相距 、竖直相距 , 求 运动到 D 点时速度的大小和改变后 P 的质量。
用插针法测量上、下表面平行的玻璃砖的折射率。实验中用A、B两个大头针确定入射光路,C、D两个大头针确定出射光路, 和 分别是入射点和出射点。如图(a)所示。测得玻璃砖厚度为 ;A到过 点的法线 的距离 , 到玻璃砖的距离 , 到 的距离为 。
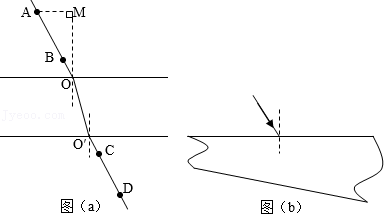
(ⅰ)求玻璃砖的折射率;
(ⅱ)用另一块材料相同,但上下两表面不平行的玻璃砖继续实验,玻璃砖的截面如图(b)所示。光从上表面入射,入射角从 逐渐增大,达到 时,玻璃砖下表面的出射光线恰好消失。求此玻璃砖上下表面的夹角。
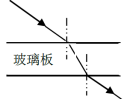
(1)如图,单色光从折射率 n=1.5、厚度 d=10.0 cm的玻璃板上表面射入。已知真空中的光速为3.0×10 8m/s,则该单色光在玻璃板内传播的速度为_________m/s;对于所有可能的入射角,该单色光通过玻璃板所用时间 t的取值范围是__________s≤ t<_________s(不考虑反射)。
(2)均匀介质中质点 A、 B的平衡位置位于 x轴上,坐标分别为0和 x B=16 cm。某简谐横波沿 x轴正方向传播,波速为 v=20 cm/s,波长大于20 cm,振幅为 y=l cm,且传播时无衰减。 t=0时刻 A、 B偏离平衡位置的位移大小相等、方向相同,运动方向相反,此后每隔Δ t=0.6 s两者偏离平衡位置的位移大小相等、方向相同。已知在 t 1时刻( t 1>0),质点 A位于波峰。求:
(i)从 t 1时刻开始,质点 B最少要经过多长时间位于波峰;
(ii) t 1时刻质点 B偏离平衡位置的位移。
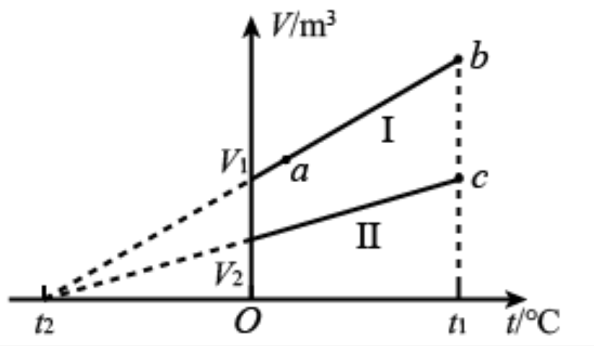
(1)如图,一定量的理想气体经历的两个不同过程,分别由体积-温度(V-t)图上的两条直线I和Ⅱ表示, V 1和 V 2分别为两直线与纵轴交点的纵坐标; t 0为它们的延长线与横轴交点的横坐标, t 0=-273.15°C; a为直线I上的一点。由图可知,气体在状态 a和 b的压强之比 p a/ p b=______;气体在状态 b和 c的压强之比 p a/ p c=_________。
(2)如图,一汽缸中由活塞封闭有一定量的理想气体,中间的隔板将气体分为 A、 B两部分;初始时, A、 B的体积均为 V,压强均等于大气压 p 0。隔板上装有压力传感器和控制装置,当隔板两边压强差超过0.5 p 0时隔板就会滑动,否则隔板停止运动。气体温度始终保持不变。向右缓慢推动活塞,使 B的体积减小为 V/2。
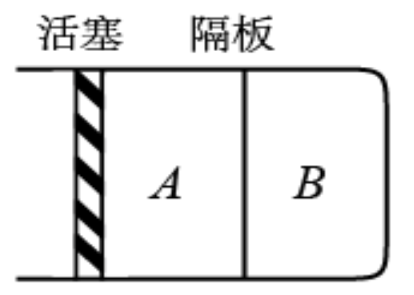
(i)求 A的体积和 B的压强;
(ⅱ)再使活塞向左缓慢回到初始位置,求此时 A的体积和 B的压强。
如图,长度均为 l的两块挡板竖直相对放置,间距也为 l,两挡板上边缘 P和 M处于同一水平线上,在该水平线的上方区域有方向竖直向下的匀强电场,电场强度大小为 E;两挡板间有垂直纸面向外、磁感应强度大小可调节的匀强磁场。一质量为 m,电荷量为 q( q>0)的粒子自电场中某处以大小为v 0的速度水平向右发射,恰好从 P点处射入磁场,从两挡板下边缘 Q和 N之间射出磁场,运动过程中粒子未与挡板碰撞。已知粒子射入磁场时的速度方向与 PQ的夹角为60°,不计重力。
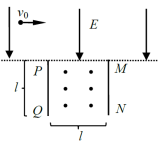
(1)求粒子发射位置到 P点的距离;
(2)求磁感应强度大小的取值范围;
(3)若粒子正好从 QN的中点射出磁场,求粒子在磁场中的轨迹与挡板 MN的最近距离。
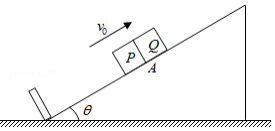
如图所示,一倾角为 的固定斜面的底端安装一弹性挡板, 、 两物块的质量分别为 和 , 静止于斜面上 处。某时刻, 以沿斜面向上的速度 与 发生弹性碰撞。 与斜面间的动摩擦因数等于 ,设最大静摩擦力等于滑动摩擦力。 与斜面间无摩擦,与挡板之间的碰撞无动能损失。两物块均可以看作质点,斜面足够长, 的速度减为零之前 不会与之发生碰撞。重力加速度大小为 。
(1)求 与 第一次碰撞后瞬间各自的速度大小 、 ;
(2)求第 次碰撞使物块 上升的高度 ;
(3)求物块 从 点上升的总高度 ;
(4)为保证在 的速度减为零之前 不会与之发生碰撞,求 点与挡板之间的最小距离 。
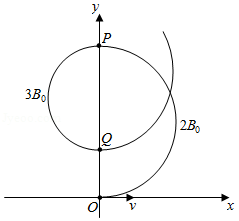
空间存在两个垂直于 平面的匀强磁场, 轴为两磁场的边界,磁感应强度分别为 、 .甲、乙两种比荷不同的粒子同时从原点 沿 轴正向射入磁场,速度均为 。甲第1次、第2次经过 轴的位置分别为 、 ,其轨迹如图所示。甲经过 时,乙也恰好同时经过该点。已知甲的质量为 ,电荷量为 。不考虑粒子间的相互作用和重力影响。求:
(1) 到 的距离 ;
(2)甲两次经过 点的时间间隔△ 。
(3)乙的比荷 可能的最小值。
如图所示,一轻绳吊着粗细均匀的棒,棒下端离地面高H,上端套着一个细环,棒和环的质量均为m,相互间最大静摩擦力等于滑动摩擦力kmg(k>1)。断开轻绳,棒和环自由下落。假设棒足够长,与地面发生碰撞时,触地时间极短,无动能损失.棒在整个运动过程中始终保持竖直,空气阻力不计。求:
(1)从断开轻绳到棒和环都静止,摩擦力对环及棒做的总功W.
(2)从断开轻绳到棒和环都静止,棒运动的总路程s.
如图甲所示,有一倾角为300的光滑固定斜面,斜面底端的水平面上放一质量为M的木板.开始时质量为m =1kg的滑块在水平向左的力F作用下静止在斜面上,今将水平力F变为水平向右大小不变,当滑块滑到木板上时撤去力F(假设斜面与木板连接处用小圆弧平滑连接)。此后滑块和木板在水平上运动的v-t图象如图乙所示,g=10 m/s2.求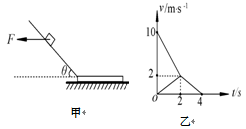
(1)水平作用力F的大小;
(2)滑块开始下滑时的高度;
(3)木板的质量。
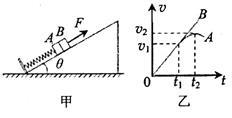
如图甲所示,平行于光滑斜面的轻弹簧劲度系数为k,一端固定在倾角为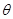 的斜面底端,另一端与物块A连接;两物块A、B质量均为m,初始时均静止。现用平行于斜面向上的力F拉动物块B,使B做加速度为a的匀加速运动,A、B两物块在开始一段时间内的v-t关系分别对应图乙中A、B图线(t1时刻A、B的图线相切,t2时刻对应A图线的最高点),重力加速度为g,则( )
的斜面底端,另一端与物块A连接;两物块A、B质量均为m,初始时均静止。现用平行于斜面向上的力F拉动物块B,使B做加速度为a的匀加速运动,A、B两物块在开始一段时间内的v-t关系分别对应图乙中A、B图线(t1时刻A、B的图线相切,t2时刻对应A图线的最高点),重力加速度为g,则( )
A.t2时刻,弹簧形变量为0
B.t1时刻,弹簧形变量为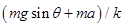
C.从开始到t2时刻,拉力F逐渐增大
D.从开始到t1时刻,拉力F做的功比弹簧弹力做的功少