高中物理试题

随着我国经济和科技的发展，通过引进、创先、研发后，我国具有知识产权的大型运输机已试飞成功，此机可在短时间内投放物资和人员进行救灾、抢险和军事活动，能争取更多时间。现有总质量为一架大型喷气式飞机，从静止开始保持额定功率滑跑，当位移达到时，速度达到最大速度，并以此速度起飞，在此过程中飞机受到的平均阻力是飞机重力的0.02倍（）求：
（1）飞机起飞时的动能为多大？
（2）飞机起飞时的功率P为多大？
（3）飞机的速度为30m/s时加速度为多大？

某同学通过设计实验探究绕轴转动而具有的动能与哪些因素有关。他以圆形砂轮为研究对象，研究其转动动能与质量、半径、角速度的具体关系。砂轮由动力带动匀速旋转测得其角速度ω，然后让砂轮脱离动力，用一把弹性尺子与砂轮接触使砂轮慢慢停下，设尺子与砂轮间的摩擦力大小恒为10/π牛（不计转轴与砂轮的摩擦），分别取不同质量、不同半径的砂轮，使其以不同的角速度旋转进行实验，得到数据如下表所示：
（1）由上述数据推导出转动动能E_k与质量m、角速度ω、半径r的关系式                          为        (比例系数用k表示）。合理猜想K的值为       单位      （填“有”或“没有”）
（2）以上实验运用了物理学中的一个重要的实验方法是          。

半径r/cm	质量m/kg	角速度ω(rad/s)	转动动能Ek/J
4	1	2	6.4
4	1	3	14.4
4	1	4	25.6
4	2	2	12.8
4	3	2	19．2
4	4	2	25.6
8	1	2	25.6
12	1	2	57.6
16	1	2	102．4

 

某同学为了测定一根轻弹簧压缩到最短时具有的弹性势能的大小，将弹簧的一端固定在光滑水平桌面上，如图所示，用已知质量为m的钢球将弹簧压缩至最短，而后突然释放，弹簧的弹性势能转化为钢球的动能，钢球将沿水平方向飞出桌面，实验时:

（1）还需要测定的物理量及物理量的符号是           ,                ；
（2）计算弹簧最短时弹性势能的关系式是＝              。

火星表面特征非常接近地球，适合人类居住。近期，我国宇航员王跃正与俄罗斯宇航员一起进行“模拟登火星”实验活动。已知火星的半径是地球半径的1/2，质量是地球质量的1/9，自转周期也基本与地球的自转周期相同。地球表面重力加速度是g，若王跃在地面上能竖直向上跳起的最大高度是h。在忽略自转影响的条件下，下述分析正确的是（   ）

A．王跃在火星表面受到的万有引力是他在地球表面所受万有引力的4/9倍

B．火星表面的重力加速度是2/9g

C．火星的第一宇宙速度是地球第一宇宙速度的/3倍

D．王跃以相同的初速度在火星上竖直起跳时，能上升的最大高度是9h/4

质量为m的物体在空中由静止下落，由于空气阻力，运动的加速度是0.9g，物体下落高度为h，以下说法正确的是（  ）

A．重力势能减小了0.9mgh	B．动能增大了0.9mgh
C．动能增大了0.1mgh	D．机械能损失了0.1mgh

在发射地球同步卫星的过程中，卫星首先进入椭圆轨道Ⅰ，然后在Q点通过改变卫星速度，让卫星进入地球同步轨道Ⅱ．则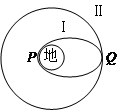

A．该卫星的发射速度必定大于第二宇宙速度11.2km/s

B．卫星在同步轨道Ⅱ上的运行速度大于第一宇宙速度7.9km/s

C．在轨道Ⅰ上，卫星在P点的速度大于在Q点的速度

D．卫星在Q点通过加速实现由轨道Ⅰ进入轨道Ⅱ

如图甲所示，轻杆一端固定在O点，另一端固定一小球，现让小球在竖直平面内做半径为R的圆周运动。小球运动到最高点时，杆与小球间弹力大小为F，小球在最高点的速度大小为v，其F一v²图象如图乙所示。不计空气阻力，则  （     ）

A．小球的质量为

B．当地的重力加速度大小为

C．v^2=c时，杆对小球的弹力方向向上

D．v^2=2b时，小球受到的弹力与重力大小不相等

在同一高度，把三个质量相同的球A，B，C分别以相等的速率竖直上抛，竖直下抛和平抛，它们都落到同一水平地面上，则三个球在运动过程中，重力对它们做的功分别为W_A，W_B，W_C，重力的平均功率分别为P_A，P_B，P_C，则它们的大小关系为（ ）
A，W_A＞W_B＞W_C，P_A＞P_B=P_C      B．W_A=W_B=W_C，P_A=P_B=P_C
C．W_A=W_B=W_C，P_B＞P_C＞P_A       D．W_A＞W_B＞W_C，P_A＞P_B＞P_C

一汽车的额定功率为P，设在水平公路行驶所受的阻力恒定，最大行驶速度为v_m。则（ ）

A．若汽车以额定功率启动，则做匀加速直线运动

B．若汽车匀加速启动，则在刚达到额定功率时的速度等于vm

C．无论汽车以哪种方式启动，加速度与牵引力成正比

D．汽车以速度vm匀速行驶，若要减速，则要减少牵引力

已知万有引力常量G，下列数据不能够估算出地球的质量的是(   ）

A．月球绕地球运行的周期与月地之间的距离

B．地球表面的重力加速度与地球的半径

C．绕地球运行卫星的周期与线速度

D．近地卫星的周期与地球的密度

关于相对地面静止的通讯卫星，下列说法不正确的是（    ）

A．所有通讯卫星绕地球运动的周期都相同

B．所有通讯卫星绕地球运动的线速度都相同

C．所有通讯卫星都在地球赤道的上方

D．理论上有三颗通信卫星，就几乎可以覆盖整个地球表面

有关圆周运动的基本模型，下列说法正确的是（  ）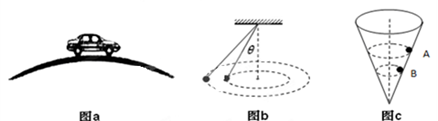

A．如图a，汽车通过拱桥的最高点处于超重状态
B．如图b所示是一圆锥摆，增大θ，但保持圆锥的高不变，则圆锥摆的角速度不变
C．如图c，同一小球在光滑而固定的圆锥筒内的A、B位置先后分别做匀度圆周运动，则在A、B两位置小球的角速度及所受筒壁的支持力大小相等
D．火车转弯超过规定速度行驶时，内轨对内轮缘会有挤压作用

如图所示，光滑的杆MN水平固定，物块A穿在杆上，可沿杆无摩擦滑动，A通过长度为L的轻质细绳与物块B相连，A、B质量均为m且可视为质点。一质量也为m的子弹水平射入物块B后未穿出，若杆足够长，此后运动过程中绳子偏离竖直方向的最大夹角为60°。求子弹刚要射入物块B时的速度大小。

从1907年起，美国物理学家密立根开始以精湛的技术测量光电效应中几个重要的物理量。他通过如图所示的实验装置测量某金属的遏止电压U_c与入射光频率ν，作出U_c－ν的图像，由此算出普朗克常量h，并与普朗克根据黑体辐射测出的h相比较，以检验爱因斯坦光电效应方程的正确性。图中频率ν₁、ν₂，遏止电压U_c1、U_c2及电子的电荷量e均为已知，求：

(1)普朗克常量h；
(2)该金属的截止频率ν₀。

探究加速度与力的关系装置如图所示。带滑轮的长木板水平放置，细绳通过两光滑滑轮分别与弹簧秤挂钩和沙桶连接，细线与桌面平行．将木块放在靠近打点计时器的一端，缓慢向沙桶中添加细沙，直到木块开始运动，记下木块运动后弹簧秤的示数F，通过纸带求出木块运动的加速度a。将木块放回原处，向沙桶中添加适量细沙，释放木块……，如此重复，获取多组a、F数据。

（1）关于该实验的操作，以下说法正确的是          

A．实验过程中，应先闭合打点计时器开关，再释放小车

B．通过缓慢添加细沙，可以方便地获取多组实验数据

C．每次添加细沙后，需测出沙及沙桶的质量

D．实验过程要确保沙及沙桶的质量远小于木块的质量

（2）某同学根据实验数据做出了两个a-F图象如图所示，正确的是        ；已知图线与横轴的交点为F₀，则木块所受的滑动摩擦力大小为       。