从1907年起，美国物理学家密立根开始以精湛的技术测量光电效应中几个重要的物理量。他通过如图所示的实验装置测量某金属的遏止电压Uc与入射光频率ν，作出Uc－ν的图像，由此算出普朗克常量h，并与普朗克根据黑体辐射测出的h相比较，以检验爱因斯坦光电效应方程的正确性。图中频率ν1、ν2，遏止电压Uc1、Uc2及电子的电荷量e均为已知，求：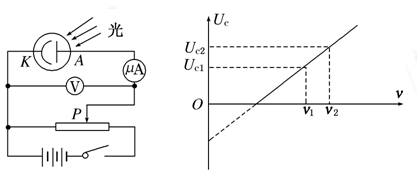
(1)普朗克常量h；
(2)该金属的截止频率ν0。
相关试题
汽车做匀加速直线运动，初速度为10m/s，若它在开始的10s内位移为175m，求：
(1)它的加速度；
(2)在离出发点52m处的速度大小；
(3)第7s内的位移大小.
如图所示，两平行金属板水平放置,板间存在着如图所示的交变电场，极板长为L，板间距离为d，取竖直向上的方向为电场强度的正方向。一带电量为q的正电荷从两板正中间的位置由左侧射入板间，初速度为v0，已知电荷所受电场力大小是其重力的2倍，重力加速度为g，且0时刻射入的粒子正好可从
板间射出。求：
(1)两板间距d应满足的条件
(2)0时刻射入的粒子射出板间时的动能
如图所示的电路中，R1=10Ω，R2=4Ω，R3=6Ω，R4=3Ω，U=2.4V。在 ab间接一只理想电压表，它的读数是多少？如在ab间接一只理想电流表，它的读数又是多少？
粤公网安备 44130202000953号