(本题满分18分,其中第1小题5分,第2小题5分,第3小题8分)
在平面直角坐标系中,已知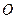 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中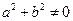 且
且 .设
.设 .
.
(1)若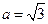 ,
,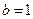 ,
, ,求方程
,求方程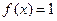 在区间
在区间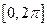 内的解集;
内的解集;
(2)若点 是过点
是过点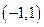 且法向量为
且法向量为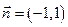 的直线
的直线 上的动点.当
上的动点.当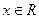 时,设函数
时,设函数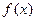 的值域为集合
的值域为集合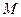 ,不等式
,不等式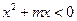 的解集为集合
的解集为集合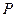 . 若
. 若 恒成立,求实数
恒成立,求实数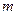 的最大值;
的最大值;
(3)根据本题条件我们可以知道,函数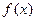 的性质取决于变量
的性质取决于变量 、
、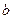 和
和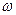 的值. 当
的值. 当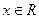 时,试写出一个条件,使得函数
时,试写出一个条件,使得函数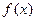 满足“图像关于点
满足“图像关于点 对称,且在
对称,且在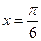 处
处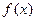 取得最小值”.(说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.)
取得最小值”.(说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.)
(本题满分18分,其中第1小题6分,第2小题4分,第3小题8分)
定义变换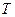 :
: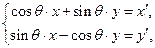 可把平面直角坐标系上的点
可把平面直角坐标系上的点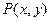 变换到这一平面上的点
变换到这一平面上的点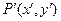 .特别地,若曲线
.特别地,若曲线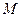 上一点
上一点 经变换公式
经变换公式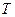 变换后得到的点
变换后得到的点 与点
与点 重合,则称点
重合,则称点 是曲线
是曲线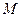 在变换
在变换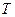 下的不动点.
下的不动点.
(1)若椭圆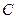 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在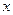 轴上,且焦距为
轴上,且焦距为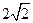 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆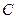 的标准方程. 并求出当
的标准方程. 并求出当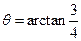 时,其两个焦点
时,其两个焦点 、
、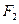 经变换公式
经变换公式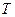 变换后得到的点
变换后得到的点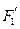 和
和 的坐标;
的坐标;
(2)当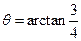 时,求(1)中的椭圆
时,求(1)中的椭圆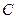 在变换
在变换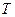 下的所有不动点的坐标;
下的所有不动点的坐标;
(3)试探究:中心为坐标原点、对称轴为坐标轴的双曲线在变换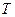 :
: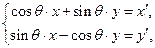 (
( ,
,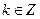 )下的不动点的存在情况和个数.
)下的不动点的存在情况和个数.
(本题满分14分,其中第1小题8分,第2小题6分)
一企业生产的某产品在不做电视广告的前提下,每天销售量为 件. 经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量
件. 经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量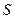 (件)与电视广告每天的播放量
(件)与电视广告每天的播放量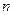 (次)的关系可用如图所示的程序框图来体现.
(次)的关系可用如图所示的程序框图来体现.
(1)试写出该产品每天的销 售量
售量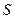 (件)关于电视广告每天的播放量
(件)关于电视广告每天的播放量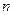 (次)的函数关系式;
(次)的函数关系式;
(2)要使该产品每天的销售量比不做电视广告时的销售量至少增加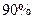 ,则每天电视广告的播放量至少需多少次?
,则每天电视广告的播放量至少需多少次?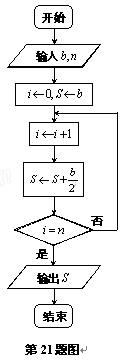
已知 ,
,
命题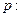 实系数一元二次方程
实系数一元二次方程
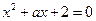 的两根都是虚数;
的两根都是虚数;
命题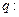 存在复数
存在复数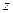 同时满足
同时满足 且
且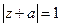 .
.
试判断:命题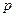 和命题
和命题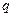 之间是否存在推出关系?请说明你的理由.
之间是否存在推出关系?请说明你的理由.
(本题满分18分,其中第1小题6分,第2小题4分,第3小题8分)
现有变换公式 :
: 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点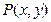 变换到这一平面上的一点
变换到这一平面上的一点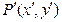 .
.
(1)若椭圆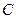 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在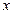 轴上,且焦距为
轴上,且焦距为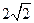 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆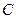 的标准方程,并求出其两个焦点
的标准方程,并求出其两个焦点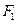 、
、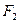 经变换公式
经变换公式 变换后得到的点
变换后得到的点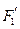 和
和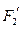 的坐标;
的坐标;
(2) 若曲线 上一点
上一点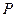 经变换公式
经变换公式 变换后得到的点
变换后得到的点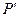 与点
与点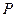 重合,则称点
重合,则称点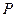 是曲线
是曲线 在变换
在变换 下的不动点. 求(1)中的椭圆
下的不动点. 求(1)中的椭圆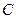 在变换
在变换 下的所有不动点的坐标;
下的所有不动点的坐标;
(3) 在(2)的基础上,试探究:中心为坐标原点、对称轴为坐标轴的椭圆和双曲线在变换 下的不动点的存在情况和个数.
下的不动点的存在情况和个数.
(本题满分18分,其中第1小题6分,第2小题6分,第3小题6分)
已知数列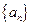 的首项为1,前
的首项为1,前 项和为
项和为 ,且满足
,且满足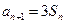 ,
,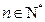 .数列
.数列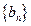 满足
满足 .
.
(1) 求数列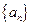 的通项公式;
的通项公式;
(2) 当 时,试比较
时,试比较 与
与 的大小,并说明理由;
的大小,并说明理由;
(3) 试判断:当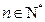 时,向量
时,向量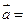
 是否可能恰为直线
是否可能恰为直线
 的方向向量?请说明你的理由.
的方向向量?请说明你的理由.
(本题满分14分,其中第1小题8分,第2小题6分)
一企业生产的某产品在不做电视广告的前提下,每天销售量为 件. 经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量
件. 经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量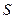 (件)与电视广告每天的播放量
(件)与电视广告每天的播放量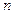 (次)的关系可用如图所示的程序框图来体现.
(次)的关系可用如图所示的程序框图来体现.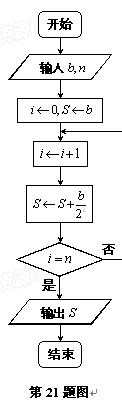
(1)试写出该产品每天的销售量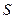 (件)关于电视广告每天的播放量
(件)关于电视广告每天的播放量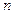 (次)的函数关系式;
(次)的函数关系式;
(2)要使该产品每天的销售量比不做电视广告时的销售量至少增加 ,则每天电视广告的播放量至少需多少次?
,则每天电视广告的播放量至少需多少次?
(本题满分18分,第(1)小题4分,第(2)小题6分,第(2)小题8分)
已知双曲线C: 的一个焦点是
的一个焦点是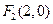 ,且
,且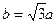 。
。
(1)求双曲线C的方程;
(2)设经过焦点 的直线
的直线 的一个法向量为
的一个法向量为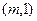 ,当直线
,当直线
 与双曲线C的右支相交于
与双曲线C的右支相交于 不同的两点时,求实数
不同的两点时,求实数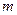 的取值范围;并证明
的取值范围;并证明 中点
中点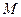 在曲线
在曲线 上。
上。
(3)设(2)中直线 与双曲线C的右支相交于
与双曲线C的右支相交于 两点,问是否存在实数
两点,问是否存在实数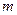 ,使得
,使得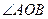 为锐角?若存在,请求出
为锐角?若存在,请求出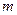 的范围;若不存在,请说明理由。
的范围;若不存在,请说明理由。
(本题满分16分,第(1)小题4分,第(2)小题6分,第(2)小题6分)
在平行四边形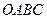 中,已知过点
中,已知过点 的直线与线段
的直线与线段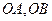 分别相交于点
分别相交于点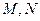 。若
。若 。
。
(1)求证: 与
与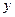 的关系为
的关系为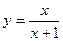 ;
;
(2)设 ,定义在
,定义在 上的偶函数
上的偶函数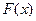 ,当
,当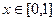 时
时 ,且函数
,且函数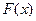 图象关于直线
图象关于直线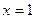 对称,求证:
对称,求证: ,
, 并求
并求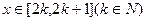 时的解析式;
时的解析式;
(3)在(2)的条件下,不等式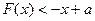 在
在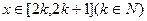 上恒成立,求实数
上恒成立,求实数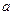 的取值范围。
的取值范围。
(本题满分16分,第(1)小题4分,第(2)小题6分,第(2)小题6分)
设数列 中,若
中,若 ,则称数列
,则称数列 为“凸数列”。
为“凸数列”。
(1)设数列 为“凸数列”,若
为“凸数列”,若 ,试写出该数列的前6项,并求出该6项之和;
,试写出该数列的前6项,并求出该6项之和;
(2)在“凸数列” 中,求证:
中,求证: ;
;
(3)设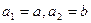 ,若数列
,若数列 为“凸数列”,求数列前2010项和
为“凸数列”,求数列前2010项和 。
。
(本题满分14分,第(1)小题6分,第(2)小题8分)
设 分别为
分别为 的内角
的内角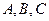 的对边,
的对边,
 与
与 的夹角为
的夹角为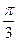
(1)求角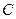 的大小;
的大小;
(2)已知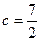 ,
, 的面积
的面积 ,求
,求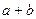 的值。
的值。
(本题满分14分,第(1)小题6分,第(2)小题8分)
设函数 ,若不等式
,若不等式 的解集为
的解集为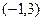 。
。 (1)求
(1)求 的值;
的值;
(2)若函数 在
在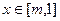 上的最小值为1,求实数
上的最小值为1,求实数 的值。
的值。