上海市普陀区高三第二次模拟考试数学文
某企业投资72万元兴建一座环保建材厂. 第1年各种经营成本为12万元,以后每年的经营成本增 加4万元,每年销售环保建材的收入为50万元. 则该厂获取的纯利润达到最大值时是在第 年.
加4万元,每年销售环保建材的收入为50万元. 则该厂获取的纯利润达到最大值时是在第 年.
(本题满分14分,其中第1小题8分,第2小题6分)
一企业生产的某产品在不做电视广告的前提下,每天销售量为 件. 经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量
件. 经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量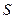 (件)与电视广告每天的播放量
(件)与电视广告每天的播放量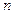 (次)的关系可用如图所示的程序框图来体现.
(次)的关系可用如图所示的程序框图来体现.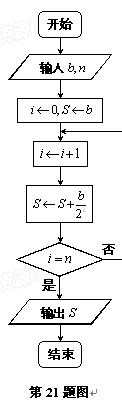
(1)试写出该产品每天的销售量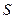 (件)关于电视广告每天的播放量
(件)关于电视广告每天的播放量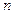 (次)的函数关系式;
(次)的函数关系式;
(2)要使该产品每天的销售量比不做电视广告时的销售量至少增加 ,则每天电视广告的播放量至少需多少次?
,则每天电视广告的播放量至少需多少次?
(本题满分18分,其中第1小题6分,第2小题6分,第3小题6分)
已知数列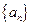 的首项为1,前
的首项为1,前 项和为
项和为 ,且满足
,且满足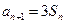 ,
,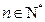 .数列
.数列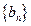 满足
满足 .
.
(1) 求数列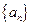 的通项公式;
的通项公式;
(2) 当 时,试比较
时,试比较 与
与 的大小,并说明理由;
的大小,并说明理由;
(3) 试判断:当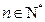 时,向量
时,向量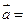
 是否可能恰为直线
是否可能恰为直线
 的方向向量?请说明你的理由.
的方向向量?请说明你的理由.
 ,则
,则 .
. 的图像关于原点对称,且存在反函数
的图像关于原点对称,且存在反函数 . 若已知
. 若已知 ,则
,则 .
. 的定义域是 .
的定义域是 . ,
, ,则
,则 .
. 所表示的平面区域的面积是 .
所表示的平面区域的面积是 .
 ,则方程
,则方程 的解集为 .
的解集为 . 的解集为 .
的解集为 . 描述,敲击一次音叉B所发出的声波可用函数
描述,敲击一次音叉B所发出的声波可用函数 描述,则两个音叉所发出的音量较大的是 .(填入A或B)
描述,则两个音叉所发出的音量较大的是 .(填入A或B) 上的点所对应的复数
上的点所对应的复数 满足
满足 ,则直线
,则直线 的两条对角线相交于点
的两条对角线相交于点 ,点
,点 是
是 的中点. 若
的中点. 若 ,
,  ,且
,且 ,则
,则 .
. 
 ,
, ,且
,且 (
( ).当
).当 时,点
时,点 无限趋近于点
无限趋近于点 ,则点
,则点 的展开式中任取
的展开式中任取 项,则取出的
项,则取出的 ,条件
,条件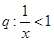 ,则
,则 是
是 成立的 ( )
成立的 ( ) 上的点到定点
上的点到定点 和到定直线
和到定直线 的距离相等,
的距离相等, ( )
( ) ;
; ;
; ;
; .
. ;
; ;
;
 ;
; .
. (
( )的零点都在区间[-10,10]上,则使得方程
)的零点都在区间[-10,10]上,则使得方程 有正整数解的实数
有正整数解的实数 的取值个数为 ( )
的取值个数为 ( )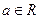 ,且以下命题都为真命题:
,且以下命题都为真命题: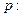 实系数一元二次方程
实系数一元二次方程 的两根都是虚数;
的两根都是虚数;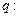 存在复数
存在复数 同时满足
同时满足 且
且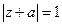 .
. 的取值范围.
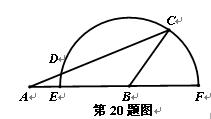
的取值范围.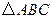 中,
中, ,
,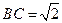 ,
,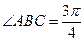 . 以
. 以 点
点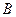 为圆心,线段
为圆心,线段 的长为半径的半圆分别交
的长为半径的半圆分别交 所在直线于点
所在直线于点 、
、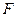 ,交线段
,交线段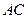 于点
于点 ,求弧
,求弧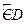 的长.(精确到
的长.(精确到 )
)
 :
: 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点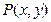 变换到这一平面上的一点
变换到这一平面上的一点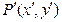 .
.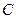 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在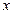 轴上,且焦距为
轴上,且焦距为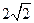 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆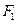 、
、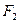 经变换公式
经变换公式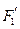 和
和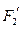 的坐标;
的坐标; 上一点
上一点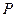 经变换公式
经变换公式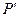 与点
与点 粤公网安备 44130202000953号
粤公网安备 44130202000953号