(本题满分14分,其中第1小题8分,第2小题6分)
一企业生产的某产品在不做电视广告的前提下,每天销售量为 件. 经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量
件. 经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量 (件)与电视广告每天的播放量
(件)与电视广告每天的播放量 (次)的关系可用如图所示的程序框图来体现.
(次)的关系可用如图所示的程序框图来体现.
(1)试写出该产品每天的销售量 (件)关于电视广告每天的播放量
(件)关于电视广告每天的播放量 (次)的函数关系式;
(次)的函数关系式;
(2)要使该产品每天的销售量比不做电视广告时的销售量至少增加 ,则每天电视广告的播放量至少需多少次?
,则每天电视广告的播放量至少需多少次?
相关知识点
推荐套卷
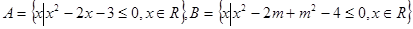
 ,求
,求 实数的值;
实数的值; ,求实数
,求实数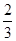 .
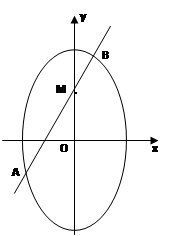
.
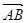 所成的比为2,求线段AB所在直线的方程.
所成的比为2,求线段AB所在直线的方程.
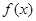 是定义域上的单调函数,求
是定义域上的单调函数,求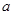 的取值范围;
的取值范围;
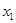 、
、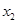 ,证明:
,证明: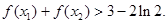
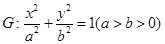 的离心率为
的离心率为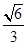 ,右焦点为(
,右焦点为(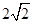 ,0),斜率为1的直线
,0),斜率为1的直线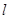 与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为
与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为 .
.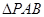 的面积.
的面积.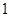 次,求在这一枪出现空弹的概率;
次,求在这一枪出现空弹的概率;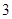 次,求在这三枪中出现空弹的概率;
次,求在这三枪中出现空弹的概率; 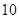 的等边
的等边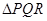 ,甲射手用实弹瞄准了三角形
,甲射手用实弹瞄准了三角形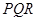 区域随机射击,且弹孔都落在三角形
区域随机射击,且弹孔都落在三角形 粤公网安备 44130202000953号
粤公网安备 44130202000953号