已知函数f(x)= (x≠﹣1).设数列{an}满足a1=1,an+1=f(an),数列{bn}满足bn=|an﹣
(x≠﹣1).设数列{an}满足a1=1,an+1=f(an),数列{bn}满足bn=|an﹣ |,Sn=b1+b2+…+bn(n∈N*).
|,Sn=b1+b2+…+bn(n∈N*).
(Ⅰ)用数学归纳法证明bn≤ ;
;
(Ⅱ)证明Sn< .
.
在数列|an|中,a1=t﹣1,其中t>0且t≠1,且满足关系式:an+1(an+tn﹣1)=an(tn+1﹣1),(n∈N+)
(1)猜想出数列|an|的通项公式并用数学归纳法证明之;
(2)求证:an+1>an,(n∈N+).
已知正项数列{an}满足:a1=1,且(n+1)an+12=nan2﹣an+1an,n∈N*
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{ }的前n项积为Tn,求证:当x>0时,对任意的正整数n都有Tn>
}的前n项积为Tn,求证:当x>0时,对任意的正整数n都有Tn> .
.
若a1≤a2≤…≤an,而b1≥b2≥…≥bn或a1≥a2≥…≥an而b1≤b2≤…≤bn,证明: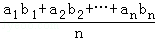 ≤(
≤(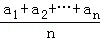 )•(
)•(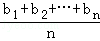 ).当且仅当a1=a2=…=an或b1=b2=…=bn时等号成立.
).当且仅当a1=a2=…=an或b1=b2=…=bn时等号成立.
设正整数构成的数列{an}使得a10k﹣9+a10k﹣8+…+a10k≤19对一切k∈N*恒成立.记该数列若干连续项的和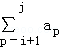 为S(i,j),其中i,j∈N*,且i<j.求证:所有S(i,j)构成的集合等于N*.
为S(i,j),其中i,j∈N*,且i<j.求证:所有S(i,j)构成的集合等于N*.
已知圆 经过椭圆Γ∶
经过椭圆Γ∶ 的右焦点F,且F到右准线的距离为2.
的右焦点F,且F到右准线的距离为2.
(1)求椭圆Γ的方程;
(2)过原点O的射线l与椭圆Γ在第一象限的交点为Q,与圆C的交点为P,M为OP的中点, 求 的最大值.
的最大值.